题目内容
已知(
+x2)2n的展开式的二项式系数和比(3x-1)n的展开式的系数和大992,
(1)求(
+
)n展开式的有理项;
(2)求(x2-
)n展开式中的系数最大的项和系数最小的项.
| 3 | x |
(1)求(
| x |
| 1 | |||
2•
|
(2)求(x2-
| 1 |
| x |
考点:二项式系数的性质,二项式定理的应用
专题:二项式定理
分析:(1)由题意可得22n-(3-1)n=992,求得n=5.在(
+
)n展开式的通项公式中,令x的幂指数为整数,求得得r的值,可得(
+
)n展开式的有理项.
(2)求出(x2-
)n的展开式的通项公式,可得第r+1项的系数,再利用二项式系数的性质求得展开式中的系数最大的项和系数最小的项.
| x |
| 1 | |||
2•
|
| x |
| 1 | |||
2•
|
(2)求出(x2-
| 1 |
| x |
解答:
解:(1)由题意可得22n-(3-1)n=992,解得2n=32,n=5.
∴(
+
)n展开式的通项公式为 Tr+1=
•(
)r•x
-
.
令
-
为整数,可得r=2,故(
+
)n展开式的有理项为 T3=
•
x=
x.
(2)求(x2-
)n=(x2-
)5展开式的通项公式为
•(-1)r•x10-3r,
故第r+1项的系数为
•(-1)r,r=0,1,2,3,4,5,
利用二项式系数的性质可得r=2时,第r+1项的系数最大,此项即T3=10x4;
检验可得r=3时,第r+1项的系数最小,此项即T4=-10x.
∴(
| x |
| 1 | |||
2•
|
| C | r 5 |
| 1 |
| 2 |
| 5 |
| 2 |
| 3r |
| 4 |
令
| 5 |
| 2 |
| 3r |
| 4 |
| x |
| 1 | |||
2•
|
| C | 2 5 |
| 1 |
| 4 |
| 5 |
| 2 |
(2)求(x2-
| 1 |
| x |
| 1 |
| x |
| C | r 5 |
故第r+1项的系数为
| C | r 5 |
利用二项式系数的性质可得r=2时,第r+1项的系数最大,此项即T3=10x4;
检验可得r=3时,第r+1项的系数最小,此项即T4=-10x.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
相关题目
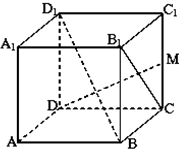 如图,正方体ABCD-A1B1C1D1中,M是CC1的中点;
如图,正方体ABCD-A1B1C1D1中,M是CC1的中点; 在长方体ABCD-A1B1C1D1中,E为AA1的中点,AB=BC=1,AA1=2.
在长方体ABCD-A1B1C1D1中,E为AA1的中点,AB=BC=1,AA1=2.