题目内容

已知函数f（x）=（x-1）2，数列{an}是各项均不为0的等差数列，且（an+1，S2n-1）在函数f（x）的图象上，数列{bn}满足：bn=（
3
4
）n-1．
（1）求an．
（2）若数列{Cn}满足：Cn=
an
4n-1bn
，令：Tn=C1+C2+…+Cn，求使Tn＜λ（n∈N+）成立的λ的取值范围．
考点：数列与不等式的综合,数列与函数的综合
专题：综合题,等差数列与等比数列
分析：（1）由题意点（an+1，S2n-1）在函数f（x）的图象上，所以an2=S2n-1，再令n=1，2求得首项和公差，从而得出通项公式an．
（2）用错位相减法求出Tn的值，即可求使Tn＜λ（n∈N+）成立的λ的取值范围．
解答： 解：（1）因为点（an+1，S2n-1）在函数f（x）的图象上，所以an2=S2n-1，
令n=1，2得
a
2
1
=S1
a
2
2
=S3
，即
a
2
1
=a1…①
a
2
2
=3a1+3d…②
，解得a1=1，d=2，
∴an=2n-1；
（2）由条件可得：Cn=
an
4n-1bn
=
2n-1
3n-1

由Tn=C1+C2+…+Cn=1+
1
30
+3•
1
3
+…+
2n-1
3n-1
①
∴
1
3
Tn=1•
1
3
+…++
2n-3
3n-1
+
2n-1
3n
②
①-②得
2
3
Tn=2-
2n+2
3n

∴Tn=3-
n+1
3n-1
＜3，
∵Tn＜λ（n∈N+）成立，
∴λ∈[3，+∞）．
点评：本题主要考查等差数列的通项公式，数列的求和，用错位相减法进行数列求和，属于中档题．
练习册系列答案
相关题目
已知函数f(x)=Asin(ωx+ϕ)(A＞0，ω＞0，|ϕ|＜
π
2
)，
（1）若cos(ϕ+
π
2
)=-
2
2
，求ϕ的值；
（2）若f（x）最大值与最小值之差等于4，其相邻两条对称轴之间的距离等于
π
3
，求函数f（x）的解析式；
（3）在（2）的条件下，求最小正实数m，使f（x）图象向右平移m个单位对应的函数是偶函数（只需写出m的值，可不写步骤）
各项均为正数的等比数列{an}，a1=1，a2a4=16，单调增数列{bn}的前n项和为Sn，b1=2，且6Sn=bn2+3bn+2（n∈N*）．
（1）求数列{an}、{bn}的通项公式；
（2）令cn=
bn
an
（n∈N*），求使得cn＞1的所有n的值，并说明理由；
（3）证明{an}中任意三项不可能构成等差数列．
经过椭圆
x2
2
+y2=1的左焦点F1作倾斜角为60°的直线l，直线l与椭圆相交于A，B两点，求AB的长．
（1）已知k，n∈N*且 k≤n，求证：k
C
k
n
=n
C
k-1
n-1
．
（2）已知数列{an}满足an=(n+2)•2n-1-1（n∈N*），是否存在等差数列{bn}，使 an=
n
k=1
bk
C
k
n
对一切n∈N*均成立？若存在，求出数列{bn}的通项公式bn；若不存在，说明理由．
已知数列{cn}满足cn=(1+
1
n
)n(n∈N*)，试证明：
（1）当n≥2时，有cn＞2；
（2）cn＜3．
两台机床同时生产一种零件，在10天中，两台机床每天的次品数如下：
甲　1，0，2，0，2，3，0，4，1，2
乙　1，3，2，1，0，2，1，1，0，1
（1）哪台机床次品数的平均数较小？
（2）哪台机床的生产状况比较稳定？
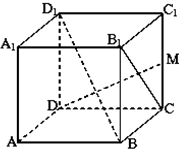如图，正方体ABCD-A1B1C1D1中，M是CC1的中点；
（1）求异面直线DM与BD1所成角的余弦值；
（2）求二面角C1-BD1-C的大小．
4张卡片的正、反两面分别写有数字0，1；2，3；4，5；6，7，将这4张卡片排成一排，可构成
 
个不同的四位偶数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网