Question

在△ABC中，已知AB=

4 6

3

，cosB=

6

6

，点D、E分别为AC、BC边的中点，且BD=

5

．
（1）求BE的长；（2）求AC的长；（3）求sinA的值．

Answer 1

考点：余弦定理,正弦定理

专题：解三角形

分析：（1）由DE为三角形ABC中位线，利用中位线定理得到DE与AB平行，其DE等于AB的一半，在三角形BDE中，设BE=x，利用余弦定理列出关于x的方程，求出方程的解得到x的值，确定出BE的长；
（2）由BE的长求出BC的长，在三角形ABC中，利用余弦定理列出关系式，将AB，BC，以及cosB的值代入求出AC的长即可；
（3）由cosB的值求出sinB的值，再由BC，AC的长，利用正弦定理求出sinA的值即可．

解答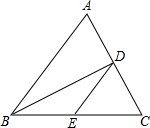： 解：（1）∵D、E分别为AC、BC边的中点，
∴DE∥AB，且DE=

1

2

AB=

2 6

3

，
设BE=x，在△BDE中，cos∠BED=-cosB=-

6

6

，
利用余弦定理可得：BD²=BE²+ED²-2BE•EDcos∠BED，即5=x²+

8

3

+2×

2 6

3

×

6

6

x，
解得：x=1或x=-

7

3

（舍去），
∴BE=1，
（2）∵BE=1，
∴BC=2BE=2，
再由余弦定理得：AC²=AB²+BC²-2AB•BCcosB=

28

3

，即AC=

2 21

3

；
（3）∵sinB=

1-cos2B

=

30

6

，BC=2，AC=

2 21

3

，
∴由正弦定理

BC

sinA

=

AC

sinB

得：sinA=

2× 30 6

2 21 3

=

70

14

．

点评：此题考查了正弦、余弦定理，以及特殊角的三角函数值，熟练掌握定理是解本题的关键．