题目内容
已知函数f(x)=2sin
x+2
cos
x.

(1)求函数f(x)的最小正周期及值域;
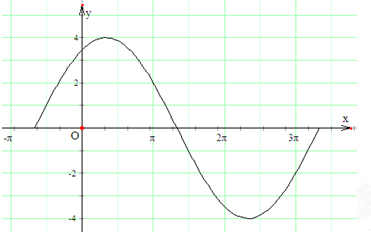
(2)试画出函数f(x)在一个周期内的简图;
(3)求函数f(x)的单调递增区间.
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |

(1)求函数f(x)的最小正周期及值域;
(2)试画出函数f(x)在一个周期内的简图;
(3)求函数f(x)的单调递增区间.
考点:三角函数中的恒等变换应用,由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:(1)利用两角和公式对函数解析式化简,进而利用周期公式求得函数的最小值正周期,利用正弦函数的性质求得函数的值域.
(2)令
x+
分别等于0,1,0,-1,0,求得x的值,通过五点描点画图.
(3)根据正弦函数的单调性,利用整体法求得函数的单调增区间.
(2)令
| 1 |
| 2 |
| π |
| 3 |
(3)根据正弦函数的单调性,利用整体法求得函数的单调增区间.
解答:
解:f(x)=4sin(
x+
).
(1)函数f(x)最小正周期T=
=4π,值域为[-4,4].
(2)列表
描点连线得函数f(x)在一个周期内的简图如下 (略)
(3)由2kπ-
≤
x+
≤2kπ+
,k∈Z,
得函数f(x)的单调递增区间为:[4kπ-
,4kπ+
],k∈Z.
| 1 |
| 2 |
| π |
| 3 |
(1)函数f(x)最小正周期T=
| 2π |
| ω |
(2)列表
| x | -
|
|
|
|
| ||||||||||
| f(x) | 0 | 1 | 0 | -1 | 0 |

(3)由2kπ-
| π |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 2 |
得函数f(x)的单调递增区间为:[4kπ-
| 5π |
| 3 |
| π |
| 3 |
点评:本题主要考查了三角函数图象与性质,三角函数恒等变换的应用.考查了学生对基础知识的综合运用.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)的离心率为2.F1、F2分别是它的左、右焦点,点A是它的右顶点.过F1作一条斜率为k(k≠0)的直线与双曲线交于两个点M、N.则∠MAN=( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、30° | B、45° |
| C、60° | D、90° |
下列命题:
①直线l与平面α无数条直线平行,则l∥α;
②若直线m在平面α外,则m∥α;
③若直线m⊥n,直线n?α内,则m⊥α;
④若直线m∥n,m?α,直线n?β内,那么平面α∥平面β;
其中真命题的个数是为( )
①直线l与平面α无数条直线平行,则l∥α;
②若直线m在平面α外,则m∥α;
③若直线m⊥n,直线n?α内,则m⊥α;
④若直线m∥n,m?α,直线n?β内,那么平面α∥平面β;
其中真命题的个数是为( )
| A、0 | B、2 | C、3 | D、4 |
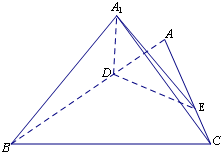 已知△ABC是边长为3的等边三角形,点D、E分别是边AB、AC上的点,且满足
已知△ABC是边长为3的等边三角形,点D、E分别是边AB、AC上的点,且满足