题目内容
在锐角△ABC中,角A,B,C的对边分别为a,b,c,且2asinB=b.
(1)求A的值;
(2)若a=2,求△ABC面积的最大值及此时b的值.
(1)求A的值;
(2)若a=2,求△ABC面积的最大值及此时b的值.
考点:正弦定理,余弦定理
专题:解三角形
分析:(1)已知等式利用正弦定理化简,根据sinB不为0求出sinA的值,即可确定出A的度数;
(2)由a,cosA的值,利用余弦定理列出关系式,再利用基本不等式变形求出bc的最大值,即可确定出三角形面积的最大值,并求出此时b的值即可.
(2)由a,cosA的值,利用余弦定理列出关系式,再利用基本不等式变形求出bc的最大值,即可确定出三角形面积的最大值,并求出此时b的值即可.
解答:
解:(1)由正弦定理得
=
化简2asinB=b,得2sinAsinB=sinB,
∵sinB≠0,
∴sinA=
,
∵△ABC是锐角三角形,
∴A=30°;
(2)∵A=30°,a=2,
∴由余弦定理得:4=b2+c2-2bccos30°=b2+c2-
bc≥(2-
)bc,
∴bc≤4(2+
),
∴S△ABC=
bcsinA≤
×4(2+
)=2+
,
当且仅当b=c=
+
时,△ABC的面积取最大值2+
.
| a |
| sinA |
| b |
| sinB |
∵sinB≠0,
∴sinA=
| 1 |
| 2 |
∵△ABC是锐角三角形,
∴A=30°;
(2)∵A=30°,a=2,
∴由余弦定理得:4=b2+c2-2bccos30°=b2+c2-
| 3 |
| 3 |
∴bc≤4(2+
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 3 |
当且仅当b=c=
| 6 |
| 2 |
| 3 |
点评:此题考查了正弦、余弦定理,以及基本不等式的运用,熟练掌握定理是解本题的关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
已知△ABC中,a=7,b=5,c=3,A=120°,则高AD=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
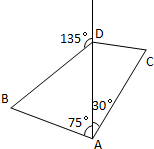 如图,某轮船从海岛A出发沿正方向航行,灯塔B在海岛A北偏西75°的方向上,且与海岛A相距
如图,某轮船从海岛A出发沿正方向航行,灯塔B在海岛A北偏西75°的方向上,且与海岛A相距