题目内容
求函数f(x)=ln
的单调递增区间.
|
考点:函数的单调性及单调区间
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:求出原函数的定义域,判断函数f(x)的奇偶性,令t=
,则y=
lnt.求出t的增区间,结合复合函数的单调性得答案.
| 1+x2 |
| 1-x2 |
| 1 |
| 2 |
解答:
解:由
>0,即1-x2>0,解得-1<x<1,
即定义域为(-1,1).
函数f(x)=ln
=
ln
,
由f(-x)=
ln
=f(x),
即有f(x)为偶函数.
令t=
,则y=
lnt.
即有t=-1+
,当0<x<1时,t递增,-1<x<0,t递减.
又y在t>0上递增,
故函数f(x)=ln
的单调递增区间为(0,1).
|
即定义域为(-1,1).
函数f(x)=ln
|
| 1 |
| 2 |
| 1+x2 |
| 1-x2 |
由f(-x)=
| 1 |
| 2 |
| 1+(-x)2 |
| 1-(-x)2 |
即有f(x)为偶函数.
令t=
| 1+x2 |
| 1-x2 |
| 1 |
| 2 |
即有t=-1+
| 2 |
| 1-x2 |
又y在t>0上递增,
故函数f(x)=ln
|
点评:本题考查了复合函数的单调性,复合函数的单调性满足同增异减的原则,应注意函数的定义域,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
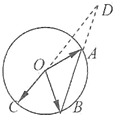 如图所示,A,B,C是圆O上的三点,CO的延长线与线段BA的延长线交于圆外的点D,若
如图所示,A,B,C是圆O上的三点,CO的延长线与线段BA的延长线交于圆外的点D,若| OC |
| OA |
| OB |
| A、(1,+∞) |
| B、(-∞,-1) |
| C、(0,1) |
| D、(-1,0) |
已知某离散型随机变量?分布列如下,则常数k的值为( )
| ? | 1 | 2 | 3 | … | n |
| P | k | 3k | 5k | … | (2n-1)k |
A、
| ||
B、
| ||
C、
| ||
D、
|
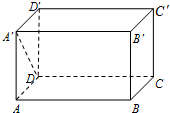 如图,在长方体ABCD-A′B′C′D′中,AB=6,AA′=BC=4,则A′D与BC所成的角等于( )
如图,在长方体ABCD-A′B′C′D′中,AB=6,AA′=BC=4,则A′D与BC所成的角等于( )| A、30° | B、45° |
| C、60° | D、90° |