题目内容
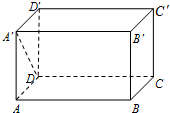如图，在长方体ABCD-A′B′C′D′中，AB=6，AA′=BC=4，则A′D与BC所成的角等于（ ）| A、30° | B、45° |
| C、60° | D、90° |
考点：异面直线及其所成的角
专题：空间角
分析：由BC∥AD，知∠A′DA是A′D与BC所成的角，由此能求出A′D与BC所成的角．
解答：
解：∵BC∥AD，
∴∠A′DA是A′D与BC所成的角，
∵AB=6，AA′=BC=4，
∴AA′=AD=4，又AA′⊥AD，
∴∠A′DA=45°．
∴A′D与BC所成的角为45°．
故选：B．
∴∠A′DA是A′D与BC所成的角，
∵AB=6，AA′=BC=4，
∴AA′=AD=4，又AA′⊥AD，
∴∠A′DA=45°．
∴A′D与BC所成的角为45°．
故选：B．
点评：本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力．在立体几何中找平行线是解决问题的一个重要技巧，这个技巧就是通过三角形的中位线找平行线，如果试题的已知中涉及到多个中点，则找中点是出现平行线的关键技巧．
练习册系列答案
阅读快车系列答案
相关题目
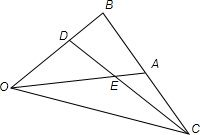如图，已知△OAB中，点C是点B关于A的对称点，点D是线段OB的一个靠近B的三等分点，DC和OA交于E，设
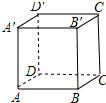如图，正方体AC′的棱长为a．已知等比数列{an}中，a2a10=9，则a5+a7（ ）
| A、有最小值6 |
| B、有最大值6 |
| C、有最小值6或最大值-6 |
| D、有最大值-6 |