题目内容
设f(x)是定义在R上的偶函数,当0≤x≤2时,y=x,当x>2时,y=f(x)的图象是顶点为P(3,4),且过点A(2,2)的抛物线的一部分.
(1)求函数f(x)在(-∞,-2)上的解析式;
(2)在直角坐标系中画出函数f(x)的草图;
(3)写出函数f(x)的值域;
(4)写出函数的单调递减区间.
(1)求函数f(x)在(-∞,-2)上的解析式;
(2)在直角坐标系中画出函数f(x)的草图;
(3)写出函数f(x)的值域;
(4)写出函数的单调递减区间.
考点:函数的图象
专题:常规题型
分析:本题考查了偶函数的图象与性质,着重考查了对应区间上函数解析式的求法,偶函数的作图方法,并涉及了其值域与单调性及抛物线的顶点式.
解答:
 (1)设顶点为P(3,4),且过点A(2,2)的抛物线的方程为y=a(x-3)2+4,
(1)设顶点为P(3,4),且过点A(2,2)的抛物线的方程为y=a(x-3)2+4,
将(2,2)代入可得a=-2,
∴y=-2(x-3)2+4,
即y=-2x2+12x-14.
设x<-2,则-x>2.
又f(x)为偶函数,
∴f(x)=f(-x)=-2×(-x)2-12x-14,
即f(x)=-2x2-12x-14.
∴函数f(x)在(-∞,-2)上的解析式为f(x)=-2x2-12x-14.
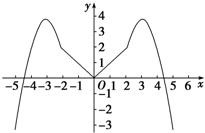
(2)函数f(x)的图象如图所示:(-3,0)
(3)由函数图象可得函数f(x)的值域为(-∞,4].
(4)由图知,递减区间为及(3,+∞)(除无穷外,其他端点也可以取到)
 (1)设顶点为P(3,4),且过点A(2,2)的抛物线的方程为y=a(x-3)2+4,
(1)设顶点为P(3,4),且过点A(2,2)的抛物线的方程为y=a(x-3)2+4,将(2,2)代入可得a=-2,
∴y=-2(x-3)2+4,
即y=-2x2+12x-14.
设x<-2,则-x>2.
又f(x)为偶函数,
∴f(x)=f(-x)=-2×(-x)2-12x-14,
即f(x)=-2x2-12x-14.
∴函数f(x)在(-∞,-2)上的解析式为f(x)=-2x2-12x-14.
(2)函数f(x)的图象如图所示:(-3,0)
(3)由函数图象可得函数f(x)的值域为(-∞,4].
(4)由图知,递减区间为及(3,+∞)(除无穷外,其他端点也可以取到)
点评:本题考查内容比较集中,是高中学习的重点,要熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设直线l经过点P(2,1),且A(0,4)、B(4,8)两点到直线l的距离相等,则直线l的方程是( )
| A、x-y-1=0 |
| B、x-y-1=0或x-y-4=0 |
| C、x+y-3=0 |
| D、x-y-1=0或x=2 |
 如图,已知一四棱锥P-ABCD的底面是边长为1的正方形,且侧棱PC⊥底面ABCD,且PC=2,E是侧棱PC上的动点
如图,已知一四棱锥P-ABCD的底面是边长为1的正方形,且侧棱PC⊥底面ABCD,且PC=2,E是侧棱PC上的动点 在△ABC中,已知
在△ABC中,已知