题目内容
已知函数f(x)=x+
-1
(1)记g(x)=f(x+1),试证明:g(x)图象关于原点对称.
(2)若方程f(x)=t(x2-2x+3)|x|有三个解,求实数t的取值范围.
| 2 |
| x-1 |
(1)记g(x)=f(x+1),试证明:g(x)图象关于原点对称.
(2)若方程f(x)=t(x2-2x+3)|x|有三个解,求实数t的取值范围.
考点:奇偶函数图象的对称性,函数恒成立问题
专题:函数的性质及应用
分析:(1)记g(x)=f(x+1),试证明:g(x)图象关于原点对称.
(2)若方程f(x)=t(x2-2x+3)|x|有三个解,求实数t的取值范围.
(2)若方程f(x)=t(x2-2x+3)|x|有三个解,求实数t的取值范围.
解答:
解:(1)∵f(x)=x+
-1
∴g(x)=f(x+1)=x+1+
-1=x+
,
则g(-x)=-x-
=-(x+
)=-g(x),
则g(x)是奇函数,则图象关于原点对称.
(2)∵f(x)=t(x2-2x+3)|x|,
∴x+
-1=t(x2-2x+3)|x|,
即
=t(x2-2x+3)|x|,
化简得t=
,即
=|x|(x-1)=
,
作出对对应的函数图象如图:
当x>0时,x(x-1)=(x-
)2-
≥-
,
∴要使方程f(x)=t(x2-2x+3)|x|有三个解,
则-
<
<0,
即t<-4
| 2 |
| x-1 |
∴g(x)=f(x+1)=x+1+
| 2 |
| x+1-1 |
| 2 |
| x |
则g(-x)=-x-
| 2 |
| x |
| 2 |
| x |
则g(x)是奇函数,则图象关于原点对称.
(2)∵f(x)=t(x2-2x+3)|x|,
∴x+
| 2 |
| x-1 |
即
| x2-2x+3 |
| x-1 |

化简得t=
| 1 |
| |x|(x-1) |
| 1 |
| t |
|
作出对对应的函数图象如图:
当x>0时,x(x-1)=(x-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∴要使方程f(x)=t(x2-2x+3)|x|有三个解,
则-
| 1 |
| 4 |
| 1 |
| t |
即t<-4
点评:本题主要考查函数奇偶性的判断,以及函数零点个数的应用,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
已知在△ABC中,∠C=90°,BC=2,则
•
=( )
| AB |
| BC |
| A、2 | B、-4 | C、-2 | D、4 |
设直线l经过点P(2,1),且A(0,4)、B(4,8)两点到直线l的距离相等,则直线l的方程是( )
| A、x-y-1=0 |
| B、x-y-1=0或x-y-4=0 |
| C、x+y-3=0 |
| D、x-y-1=0或x=2 |
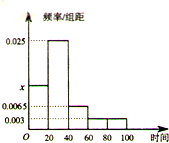 某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100).
某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100). 如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,求证:
如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,求证: 在△ABC中,已知
在△ABC中,已知