题目内容
经过点P(0,2)作直线l交椭圆
+y2=1于A,B两点.
(1)若△AOB的面积是
,求直线l的方程(其中O为原点).
(2)当△AOB的面积最大时,求直线l的方程.
| x2 |
| 2 |
(1)若△AOB的面积是
| 2 |
| 3 |
(2)当△AOB的面积最大时,求直线l的方程.
考点:椭圆的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)设直线AB:y=kx+2,代入椭圆方程,消去y,运用韦达定理,求出△AOB的面积为S=|x1-x2|,运用代入法,令S=
,解方程即可得到k;
(2)对(1)得到的S的关系式,令
=t(t>0),将分子分母除以t,再由基本不等式即可得到最大值,同时得到k,即可得到所求方程.
| 2 |
| 3 |
(2)对(1)得到的S的关系式,令
| 2k2-3 |
解答:
解:(1)设直线AB:y=kx+2,
代入椭圆方程可得,(1+2k2)x2+8kx+6=0,
设A(x1,y1),B(x2,y2),
则△=64k2-24(1+2k2)>0,即为2k2>3,
x1+x2=
,x1x2=
,
△AOB的面积为S=S△OBP-S△OAP=
•|OP|•|x1-x2|
=|x1-x2|=
=
=2
•
,
令S=
,解得,k2=
或
,
即为k=±
或±
,
则直线l:y═±
x+2或y═±
x+2;
(2)由(1)可得,
S=2
•
,
令
=t(t>0),
则2k2=3+t2,
则S=2
•
=2
•
≤2
•
=
.
当且仅当t=2即k=±
时,△AOB的面积最大,
此时直线l的方程为y=±
x+2.
代入椭圆方程可得,(1+2k2)x2+8kx+6=0,
设A(x1,y1),B(x2,y2),
则△=64k2-24(1+2k2)>0,即为2k2>3,
x1+x2=
| -8k |
| 1+2k2 |
| 6 |
| 1+2k2 |
△AOB的面积为S=S△OBP-S△OAP=
| 1 |
| 2 |
=|x1-x2|=
| (x1+x2)2-4x1x2 |
|
=2
| 2 |
| ||
| 1+2k2 |
令S=
| 2 |
| 3 |
| 5 |
| 2 |
| 11 |
| 2 |
即为k=±
| ||
| 2 |
| ||
| 2 |
则直线l:y═±
| ||
| 2 |
| ||
| 2 |
(2)由(1)可得,
S=2
| 2 |
| ||
| 1+2k2 |
令
| 2k2-3 |
则2k2=3+t2,
则S=2
| 2 |
| t |
| 4+t2 |
| 2 |
| 1 | ||
t+
|
| 2 |
| 1 | ||||
2
|
| ||
| 2 |
当且仅当t=2即k=±
| ||
| 2 |
此时直线l的方程为y=±
| ||
| 2 |
点评:本题考查椭圆的方程和性质,考查直线方程和椭圆方程联立,消去未知数,运用韦达定理,考查基本不等式的运用:求最值,考查运算能力,属于中档题.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
已知复数ω=
+
i,则ω2-ω+1=( )
| 1 |
| 2 |
| ||
| 2 |
| A、i | B、1 | C、-1 | D、0 |
在正项等比数列{an}中,lga3+lga6+lga9=6,则a5•a7的值是( )
| A、10000 | B、1000 |
| C、100 | D、10 |
将一颗质地均匀的骰子连续抛掷三次,依次得到的三个点数成等差数列的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
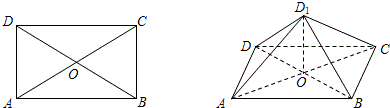
 如图甲,在平面四边形PABC中,PA=AC=2,∠P=45°,∠B=90°,
如图甲,在平面四边形PABC中,PA=AC=2,∠P=45°,∠B=90°,