题目内容
 如图甲,在平面四边形PABC中,PA=AC=2,∠P=45°,∠B=90°,
如图甲,在平面四边形PABC中,PA=AC=2,∠P=45°,∠B=90°,∠PCB=105°,现将四边形PABC沿AC折起,使平面PAC⊥平面ABC
(如图乙),D,E分别是棱PB和PC的中点.
(Ⅰ)求证:BC⊥平面PAB;
(Ⅱ)求平面ADE与平面ABC所成的锐二面角的余弦值.
考点:二面角的平面角及求法,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由已知得PA⊥AC,PA⊥平面ABC,从而PA⊥BC,又由图甲知BC⊥BA,由此能证明BC⊥平面PAB.
(Ⅱ)法一:以点B为坐标原点,分别以射线BA,BC为x,y轴,以垂直平面ABC向上方向为z轴,利用向量法能求出二面角的余弦值.
法二:以点A为坐标原点,分别以射线AC,AP为x,z轴,以垂直平面APC向外方向为y轴,利用向量法能求出二面角的余弦值.
(Ⅱ)法一:以点B为坐标原点,分别以射线BA,BC为x,y轴,以垂直平面ABC向上方向为z轴,利用向量法能求出二面角的余弦值.
法二:以点A为坐标原点,分别以射线AC,AP为x,z轴,以垂直平面APC向外方向为y轴,利用向量法能求出二面角的余弦值.
解答:
解:(Ⅰ)证明:平面PAC⊥平面ABC,并交于AC,
PA⊥AC,有PA⊥平面ABC,
故PA⊥BC,又由图甲知BC⊥BA,PA∩AB=A,
所以BC⊥平面PAB;…(6分)
(Ⅱ)解法一:如图所示,以点B为坐标原点,分别以射线BA,BC为x,y轴,
以垂直平面ABC向上方向为z轴,PA=2,则BC=1,BA=
,
A(
,0,0),P(
,0,2),C(0,1,0),
D(
,0,1),E(
,
,1),…(7分)
=(-
,0,1),
=(0,
,0),
设平面ADE的法向量为
=(x,y,z),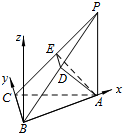
则
,
,y=0,令x=2,则z=
,
=(2,0,
),…(9分)
平面ABC的法向量
=(0,0,1),cos<
,
>=
=
=
.…(11分)
故所求二面角的余弦值为
.…(12分)
解法二:如图所示,以点A为坐标原点,分别以射线AC,AP为x,z轴,
以垂直平面APC向外方向为y轴,PA=2,
则BC=1,BA=
,A(0,0,0),P(0,0,2),B(
,
,0),
C(2,0,0),D(
,
,1),E(1,0,1),…(7分)
=(
,
,1),
=(1,0,1),
设平面ADE的法向量为
=(x,y,z),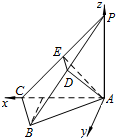
则
,
,
令x=1,则z=-1,y=
,
故
=(1,
,-1),…(9分)
平面ABC的法向量
=(0,0,1),cos<
,
>=
=
=
.…(11分)
故所求锐二面角的余弦值为
.…(12分)
PA⊥AC,有PA⊥平面ABC,
故PA⊥BC,又由图甲知BC⊥BA,PA∩AB=A,
所以BC⊥平面PAB;…(6分)
(Ⅱ)解法一:如图所示,以点B为坐标原点,分别以射线BA,BC为x,y轴,
以垂直平面ABC向上方向为z轴,PA=2,则BC=1,BA=
| 3 |
A(
| 3 |
| 3 |
D(
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| AD |
| ||
| 2 |
| DE |
| 1 |
| 2 |
设平面ADE的法向量为
| m |

则
|
|
| 3 |
| m |
| 3 |
平面ABC的法向量
| n |
| m |
| n |
| ||||
|
| ||
|
| ||
| 7 |
故所求二面角的余弦值为
| ||
| 7 |
解法二:如图所示,以点A为坐标原点,分别以射线AC,AP为x,z轴,
以垂直平面APC向外方向为y轴,PA=2,
则BC=1,BA=
| 3 |
| 3 |
| 2 |
| ||
| 2 |
C(2,0,0),D(
| 3 |
| 4 |
| ||
| 4 |
| AD |
| 3 |
| 4 |
| ||
| 4 |
| AE |
设平面ADE的法向量为
| m |

则
|
|
令x=1,则z=-1,y=
| ||
| 3 |
故
| m |
| ||
| 3 |
平面ABC的法向量
| n |
| m |
| n |
| ||||
|
| 1 | ||||
|
| ||
| 7 |
故所求锐二面角的余弦值为
| ||
| 7 |
点评:本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
已知全集U=R,集合A={x|x+1>0},B={x|y=loga(x+2)},则集合(∁UA)∩B=( )
| A、(-2,-1) |
| B、(-2,-1] |
| C、(-∞,-2) |
| D、(-1,-∞) |
已知集合A={-2,0,1,3,5},B={x∈N|-2<x≤4},则A∩B=( )
| A、{1,3} |
| B、{0,1,3} |
| C、{-1,0,1,3} |
| D、{-1,0,1,2,3,4,5} |
已知F1,F2分别是双曲线
-
=1的左、右焦点,P为双曲线右支上的任意一点,则
的最小值为( )
| x2 |
| 4 |
| y2 |
| 21 |
| |PF1|2 |
| |PF2| |
| A、24 | B、20 | C、16 | D、12 |
已知f(x)是定义在R上的函数,且f(x)的图象关于坐标原点对称;当x<0时,f(x)=-x2+2015x.若f(2-a2)+f(a)<0,则实数a的取值范围是( )
| A、(-∞,-1)∪(2,+∞) |
| B、(-∞,-2)∪(1,+∞) |
| C、(-1,2) |
| D、(-2,1) |