题目内容

如图，矩形ABCD的对角线AC，BD交于点O，AB=4，AD=3，沿AC把△ACD折起，使二面角D1-AC-B为直二面角，求二面角D1-BC-A的大小．
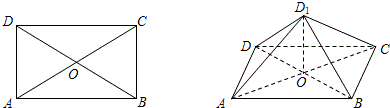
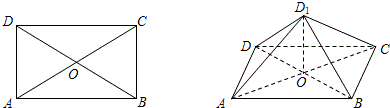
考点：二面角的平面角及求法
专题：空间角
分析：以点B为坐标原点，平面ABC为xOy平面，BC，BA方向分别为x轴，y轴的正方向，建立空间直角坐标系．利用向量法能求出二面角D1-BC-A的大小．
解答： 解：以点B为坐标原点，平面ABC为xOy平面，
BC，BA方向分别为x轴，y轴的正方向，
建立空间直角坐标系．
则B（0，0，0），C（1，0，0），A（0，2，0）．
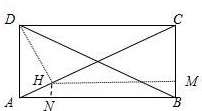
在矩形ABCD中，作DH⊥AC于H，HM⊥BC于M，HN⊥AB于N，
则H即为D1在平面ABC上的射影．
∵AB=2，AD=1，∴AC=
5
，
DH
=
2
5
，HN=
1
5
，HM=
8
5
，
∴D1（
1
5
，
8
5
，
2
5
5
），
BC
=（1，0，0），
BD1
=（
1
5
，
8
5
，
2
5
5
），
设平面D1BC的法向量为
n
=（a，b，c），
则
n
•
BC
=a=0
n
•
BD1
=a+8b+2
5
c=0
，取b=
5
，得
n
=（0，
5
，-4），
又平面ABC的法向量
m
=（0，0，1），
|cos＜
m
，
n
＞|=|
-4
5+16
|=
4
21
21
，
∴二面角D1-BC-A的大小为arccos
4
21
21
．
点评：本题考查二面角的大小的求法，是档题题，解题时要认真审题，注意向量法的合理运用．
练习册系列答案
相关题目
已知定义在R上的奇函数f（x）满足：“对于区间（0，+∞）上的任意a，b，都有f（a+b）＞f（b）成立”．
（Ⅰ）求f（0）的值，并指出f（x）在区间（0，+∞）上的单调性；
（Ⅱ）用增函数的定义证明：函数f（x）是（-∞，0）上的增函数；
（Ⅲ）判断f（x）是否为R上的增函数，如果是，请给出证明；如果不是，请举出反例．
已知α是第二象限角，且sin（
π
2
+α）=-
1
3
，则tan2α的值为（　　）
A、
4
2
7
B、-
4
2
7
C、
4
2
9
D、-
4
2
9
设F1、F2为椭圆
x2
4
+y2=1的左、右焦点，过椭圆中心任作一直线与椭圆交于P，Q两点，当四边形PF1QF2面积最大时，
PF1
•
PF2
的值等于
 
．
已知集合A={-2，0，1，3，5}，B={x∈N|-2＜x≤4}，则A∩B=（　　）
A、{1，3}
B、{0，1，3}
C、{-1，0，1，3}
D、{-1，0，1，2，3，4，5}
已知有穷数列{an}各项均不相等，将{an}的项从大到小重新排序后相应的项数构成新数列{pn}，称{pn}为{an}的“序数列”．例如数列：a1，a2，a3满足a1＞a3＞a2，则其序数列{pn}为1，3，2．
（1）若x，y∈R+，x+y=2且x≠y，写出数列：1，xy，
x2+y2
2
的序数列并说明理由；
（2）求证：有穷数列{an}的序数列{pn}为等差数列的充要条件是有穷数列{an}为单调数列；
（3）若项数不少于5项的有穷数列{bn}、{cn}的通项公式分别是bn=n•(
3
5
)n（n∈N*），cn=-n2+tn（n∈N*），且{bn}的序数列与{cn}的序数列相同，求实数t的取值范围．
已知F1，F2分别是双曲线
x2
4
-
y2
21
=1的左、右焦点，P为双曲线右支上的任意一点，则
|PF1|2
|PF2| 
的最小值为（　　）
A、24B、20C、16D、12
经过点P（0，2）作直线l交椭圆
x2
2
+y2=1于A，B两点．
（1）若△AOB的面积是
2
3
，求直线l的方程（其中O为原点）．
（2）当△AOB的面积最大时，求直线l的方程．
根据已知条件完成下列小题：
（1）已知椭圆的焦点在y轴，且a+c=20，a-c=4，求椭圆的标准方程；
（2）已知双曲线的焦点在x轴，焦距是8，离心率e=2，求双曲线的标准方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网