题目内容
已知函数f(x)=
在点(1,f(1))处的切线与x轴平行.
(Ⅰ)求实数a的值及f(x)的极值;
(Ⅱ)是否存在区间(t,t+
)(t>0),使函数f(x)在此区间上存在极值和零点?若存在,求实数t的取值范围,若不存在,请说明理由;
(Ⅲ)如果对任意的x1,x2∈[e2,+∞),有|f(x1)-f(x2)|≥k|
-
|,求实数k的取值范围.
| a+lnx |
| x |
(Ⅰ)求实数a的值及f(x)的极值;
(Ⅱ)是否存在区间(t,t+
| 2 |
| 3 |
(Ⅲ)如果对任意的x1,x2∈[e2,+∞),有|f(x1)-f(x2)|≥k|
| 1 |
| x1 |
| 1 |
| x2 |
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)由函数f(x)在(1,f(1))处的切线与x轴平行求得a的值,然后利用函数的导函数的符号求出函数的单调期间,则函数的极值可求;
(Ⅱ)假设存在区间(t,t+
)(t>0),使函数f(x)在此区间上存在极值和零点,则得到
,解此不等式组求得t的取值范围;
(Ⅲ)由(I)的结论知,f(x)在[e2,+∞)上单调递减,然后构造函数F(x)=f(x)-
,由函数在[e2,+∞)上单调递减,则其导函数在在[e2,+∞)上恒成立,由此求得实数k的取值范围.
(Ⅱ)假设存在区间(t,t+
| 2 |
| 3 |
|
(Ⅲ)由(I)的结论知,f(x)在[e2,+∞)上单调递减,然后构造函数F(x)=f(x)-
| k |
| x |
解答:
解:(I)由f(x)=
,得f′(x)=
=
.
∵f(x)在点(1,f(1))处的切线与x轴平行,
∴f′(0)=
=0,
∴a=1,
∴f(x)=
,x>0,
f′(x)=-
.
当0<x<1时,f′(x)>0,当x>1时,f′(x)<0.
∴f(x)在(0,1)上单调递增,在(1,+∞)单调递减,
故f(x)在x=1处取得极大值1,无极小值;
(Ⅱ)∵x>1时,f(x)=
>0,
当x→0时,y→-∞,
由(I)得f(x)在(0,1)上单调递增,
∴由零点存在原理,f(x)在区间(0,1)存在唯一零点,函数f(x)的图象如图所示:

∵函数f(x)在区间(t,t+
),t>0上存在极值和零点.
∴
,解得
<t<
.
∴存在符合条件的区间,实数t的取值范围为(
,
);
( III)由(I)的结论知,f(x)在[e2,+∞)上单调递减,
不妨设x1>x2≥e2,则|f(x1)-f(x2)|≥k|
-
|,则f(x2)-f(x1)≥k(
-
).
∴f(x2)-
≥f(x1)-
.
∴函数F(x)=f(x)-
在[e2,+∞)上单调递减,
又F(x)=f(x)-
=
-
,
∴F′(x)=
≤0在[e2,+∞)上恒成立,
∴k≤lnx在[e2,+∞)上恒成立.
在[e2,+∞)上(lnx)min=lne2=2,
k≤2.
| a+lnx |
| x |
| ||
| x2 |
| 1-a-lnx |
| x2 |
∵f(x)在点(1,f(1))处的切线与x轴平行,
∴f′(0)=
| 1-a-ln1 |
| 12 |
∴a=1,
∴f(x)=
| 1+lnx |
| x |
f′(x)=-
| lnx |
| x2 |
当0<x<1时,f′(x)>0,当x>1时,f′(x)<0.
∴f(x)在(0,1)上单调递增,在(1,+∞)单调递减,
故f(x)在x=1处取得极大值1,无极小值;
(Ⅱ)∵x>1时,f(x)=
| 1+lnx |
| x |
当x→0时,y→-∞,
由(I)得f(x)在(0,1)上单调递增,
∴由零点存在原理,f(x)在区间(0,1)存在唯一零点,函数f(x)的图象如图所示:

∵函数f(x)在区间(t,t+
| 2 |
| 3 |
∴
|
| 1 |
| 3 |
| 1 |
| e |
∴存在符合条件的区间,实数t的取值范围为(
| 1 |
| 3 |
| 1 |
| t |
( III)由(I)的结论知,f(x)在[e2,+∞)上单调递减,
不妨设x1>x2≥e2,则|f(x1)-f(x2)|≥k|
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| x2 |
| 1 |
| x1 |
∴f(x2)-
| k |
| x2 |
| k |
| x1 |
∴函数F(x)=f(x)-
| k |
| x |
又F(x)=f(x)-
| k |
| x |
| 1+lnx |
| x |
| k |
| x |
∴F′(x)=
| k-lnx |
| x2 |
∴k≤lnx在[e2,+∞)上恒成立.
在[e2,+∞)上(lnx)min=lne2=2,
k≤2.
点评:本题考查了利用导数研究过曲线上某点处的切线方程,考查了利用导数求函数的最值,训练了函数零点的判定方法,训练了利用恒成立问题求参数的范围,综合考查了学生的逻辑思维能力和计算能力,是压轴题.

练习册系列答案
相关题目
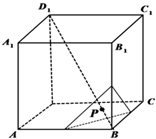 如图,正方体ABCD-A1B1C1D1的棱长为
如图,正方体ABCD-A1B1C1D1的棱长为| 3 |
| 1 |
| 2 |
| 5 |
| 2 |
A、[
| ||||||
B、[
| ||||||
C、[
| ||||||
D、[
|
从正方体ABCD-A1B1C1D1的6个表面中选取3个面,其中有2个面不相邻的选法共有( )
| A、8种 | B、12种 |
| C、16种 | D、20种 |
等比数列{an}的前n项和为Sn,若a1=1,且4a1,2a2,a3成等差数列,则S6=( )
| A、63 | B、64 | C、31 | D、32 |
已知函数f(x)=
若f(x)=2,则x的值为( )
|
| A、log32 |
| B、log23 |
| C、32 |
| D、2 |