题目内容
18.已知各项均为正数的数列{an},其前n项和为Sn,且Sn,an,$\frac{1}{2}$成等差数列,则数列{an}的通项公式为( )| A. | 2n-4 | B. | 2n-3 | C. | 2n-2 | D. | 2n-1 |
分析 Sn,an,$\frac{1}{2}$成等差数列,可得2an=Sn+$\frac{1}{2}$,利用递推关系可得:an=2an-1.利用等比数列的通项公式即可得出.
解答 解:∵Sn,an,$\frac{1}{2}$成等差数列,∴2an=Sn+$\frac{1}{2}$,
∴n=1时,2a1=a1+$\frac{1}{2}$,解得a1=$\frac{1}{2}$.
n≥2时,2an-1=Sn-1+$\frac{1}{2}$,可得:2an-2an-1=an,化为:an=2an-1.
∴数列{an}是等比数列,公比为2.
∴an=$\frac{1}{2}×{2}^{n-1}$=2n-2.
故选:C.
点评 本题考查了等差数列与等比数列的通项公式、数列递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.设(1+i)(x+yi)=2,其中x,y是实数,则|2x+yi|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
13.p:x>1,q:x>0,则p是q的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
3.设全集U={x|x<4,x∈N},A={0,1,2},B={2,3},则B∪(∁UA)等于( )
| A. | ∅ | B. | {3} | C. | {2,3} | D. | {0,1,2,3} |
10.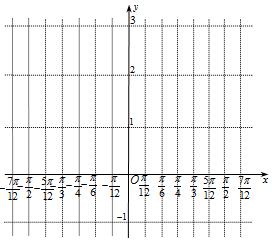 某同学用“五点法”画函数$f(x)=2sin(2x-\frac{π}{3})+1$在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象时,列表并填入了部分数据,如表:
某同学用“五点法”画函数$f(x)=2sin(2x-\frac{π}{3})+1$在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象时,列表并填入了部分数据,如表:
(1)请将上表数据补充完整,并在给出的直角坐标系中,画出f(x)在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象;
(2)利用函数的图象,直接写出函数f(x)的单调递增区间.
 某同学用“五点法”画函数$f(x)=2sin(2x-\frac{π}{3})+1$在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象时,列表并填入了部分数据,如表:
某同学用“五点法”画函数$f(x)=2sin(2x-\frac{π}{3})+1$在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象时,列表并填入了部分数据,如表:| 2x-$\frac{π}{3}$ | -$\frac{4π}{3}$ | -π | -$\frac{π}{2}$ | 0 | $\frac{π}{2}$ | $\frac{2π}{3}$ |
| x | -$\frac{π}{2}$ | -$\frac{π}{3}$ | -$\frac{π}{12}$ | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{π}{2}$ |
| f(x) |
(2)利用函数的图象,直接写出函数f(x)的单调递增区间.
 在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,过E点做EF⊥PB交PB于点F.求证:
在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,过E点做EF⊥PB交PB于点F.求证: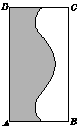 如图,面积为4的矩形ABCD中有一个阴影部分,若往矩形ABCD中随机投掷1000个点,落在矩形ABCD的非阴影部分中的点数为350个,试估计阴影部分的面积为( )
如图,面积为4的矩形ABCD中有一个阴影部分,若往矩形ABCD中随机投掷1000个点,落在矩形ABCD的非阴影部分中的点数为350个,试估计阴影部分的面积为( )