题目内容
 如图,在正方体ABCD-A1B1C1D1中,
如图,在正方体ABCD-A1B1C1D1中,(1)求证:面BB1DD1⊥面AB1C;
(2)求二面角A-B1C-D1的平面角的余弦值(理);
(3)求直线B1C与平面ABCD所成角(文).
考点:直线与平面所成的角,平面与平面垂直的判定
专题:空间角
分析:(1)根据面面垂直的判断定理即可证明面BB1DD1⊥面AB1C;
(2)根据二面角的定义先找出二面角,即可求二面角A-B1C-D1的平面角的余弦值(理);
(3)根据直线和平面所成角的定义即可求直线B1C与平面ABCD所成角(文).
(2)根据二面角的定义先找出二面角,即可求二面角A-B1C-D1的平面角的余弦值(理);
(3)根据直线和平面所成角的定义即可求直线B1C与平面ABCD所成角(文).
解答:
(1)证明:∵D1D⊥面ABCD,AC?面ABCD,
∴D1D⊥AC,
在正方形ABCD中,AC⊥BD,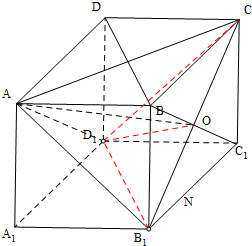
∵AC?面AB1C,
∴面BB1DD1⊥面AB1C;
(2)过点A点作AO⊥B1C交B1C于O,则O点为B1C的中点,连结D1O,D1C,
则D1B1=B1C=CD1,
∴D1O⊥B1C,
设正方体的棱长为a,连结AD1,
在△AOD中,AO=
,OD1=
,AD1=
,
由余弦定理得cos∠AOD1=
=
,
即二面角A-B1C-D1的平面角的余弦值为
;
(3)直线B1C在平面ABCD的射影为BC,
则∠B1CB是直线B1C与平面ABCD所成的角,
则∠B1CB=45°.
∴D1D⊥AC,
在正方形ABCD中,AC⊥BD,

∵AC?面AB1C,
∴面BB1DD1⊥面AB1C;
(2)过点A点作AO⊥B1C交B1C于O,则O点为B1C的中点,连结D1O,D1C,
则D1B1=B1C=CD1,
∴D1O⊥B1C,
设正方体的棱长为a,连结AD1,
在△AOD中,AO=
| ||
| 2 |
| ||
| 2 |
| 2 |
由余弦定理得cos∠AOD1=
AO2+O
| ||||
| 2AO•OD1 |
| 1 |
| 3 |
即二面角A-B1C-D1的平面角的余弦值为
| 1 |
| 3 |
(3)直线B1C在平面ABCD的射影为BC,
则∠B1CB是直线B1C与平面ABCD所成的角,
则∠B1CB=45°.
点评:本题主要考查面面垂直的判定依据空间角的求解,要求熟练相应的判断定理以及空间角的求解.

练习册系列答案
相关题目
正方体ABCD-A1B1C1D1中,M,N分别是CC1,BC的中点,则过A、M、N三点的正方体ABCD-A1B1C1D1的截面形状是( )
| A、平行四边形 | B、直角梯形 |
| C、等腰梯形 | D、以上都不对 |