题目内容
已知点M（4，1），点F为抛物线C：y2=4x的焦点，点P在抛物线上，若|PF|+|PM|取最小值，求点P的坐标．
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：由题意得到抛物线的焦点坐标和准线方程，结合抛物线定义可得过M作准线的垂线，垂线与抛物线的交点即为P点，由此求得P点的坐标．
解答：
解：由抛物线方程可知，F（1，0），准线x=-1，
如图，
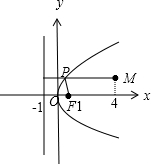M在抛物线y2=4x的内部，
根据抛物线定义知道，|PF|等于点P到准线的距离，
∴过M作准线的垂线，垂线与抛物线的交点即为P点，
∴P点纵坐标为1，由y2=4x，得x=
．
即P（
，1）．
如图，
M在抛物线y2=4x的内部，根据抛物线定义知道，|PF|等于点P到准线的距离，
∴过M作准线的垂线，垂线与抛物线的交点即为P点，
∴P点纵坐标为1，由y2=4x，得x=
| 1 |
| 4 |
即P（
| 1 |
| 4 |
点评：本题考查了抛物线的简单几何性质，考查了抛物线中的最值问题，处理这类问题的关键在于把抛物线上的点到焦点的距离转化为点到准线的距离，是中档题．
练习册系列答案
相关题目
平面区域如图所示，若使目标函数z=x+ay（a＞0）取得最大值的最优解有无穷多个，则a的值是（ ）
A、
| ||
| B、1 | ||
C、
| ||
| D、4 |
命题“?x∈R，使得x2+x+1＜0”的否定是（ ）
| A、?x∈R，均有x2+x+1＜0 |
| B、?x∈R，均有x2+x+1≥0 |
| C、?x∈R，使得 x2+x+1＜0 |
| D、?x∈R，均有x2+x+1＜0 |
如图，在正方体ABCD-A1B1C1D1中，