题目内容
1.已知函数f(x)=|2x-1|+|x+1|-a的图象与x轴有且仅有一个交点.(1)求实数a的值;
(2)若m,n∈[-a,a],求证:2|m+n|<|4+mn|
分析 (1)(x)=|2x-1|+|x+1|,去绝对值可得分段函数,画出图象可得最小值,即可得到a的值;
(2)由m,n∈[-$\frac{3}{2}$,$\frac{3}{2}$],可得m2≤$\frac{9}{4}$,n2≤$\frac{9}{4}$,运用分析法,结合平方差公式,运用不等式的性质,即可得证.
解答 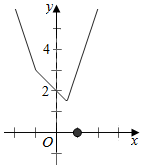 解:(1)由g(x)=|2x-1|+|x+1|=$\left\{\begin{array}{l}{-3x,x≤-1}\\{2-x,-1<x<\frac{1}{2}}\\{3x,x≥\frac{1}{2}}\end{array}\right.$,
解:(1)由g(x)=|2x-1|+|x+1|=$\left\{\begin{array}{l}{-3x,x≤-1}\\{2-x,-1<x<\frac{1}{2}}\\{3x,x≥\frac{1}{2}}\end{array}\right.$,
画出函数y=g(x)的图象,可得x=$\frac{1}{2}$时,g(x)取得最小值$\frac{3}{2}$,
由题意可得a=$\frac{3}{2}$;
(2)证明:由m,n∈[-$\frac{3}{2}$,$\frac{3}{2}$],可得m2≤$\frac{9}{4}$,n2≤$\frac{9}{4}$,
要证2|m+n|<|4+mn|,即证4(m+n)2<(4+mn)2,
即为(2m+2n+4+mn)(2m+2n-4-mn)<0,
即为(2+n)(2+m)(2-n)(-2+m)<0,
即为(4-n2)(m2-4)<0,
由m2≤$\frac{9}{4}$,n2≤$\frac{9}{4}$,可得m2<4,n2<4,
即4-m2>0,n2-4<0,
则(4-n2)(m2-4)<0成立,
故原不等式成立.
点评 本题考查绝对值函数的最值的求法,注意运用零点分区间和数形结合的思想方法,考查不等式的证明,注意运用分析法,考查推理和运算能力,属于中档题.

练习册系列答案
相关题目
6.已知角α是三角形的一个内角,若sinα>$\frac{1}{2}$,则角α的取值范围是( )
| A. | ($\frac{π}{6}$,$\frac{π}{2}$) | B. | ($\frac{π}{3}$,$\frac{π}{2}$) | C. | ($\frac{π}{6}$,$\frac{5π}{6}$) | D. | ($\frac{π}{3}$,$\frac{2π}{3}$) |
10.已知数列{an}满足anan+1=2n,则$\frac{{a}_{7}}{{a}_{3}}$=( )
| A. | 2 | B. | 4 | C. | 5 | D. | $\frac{5}{2}$ |