题目内容

10．已知数列{an}满足anan+1=2n，则$\frac{{a}_{7}}{{a}_{3}}$=（　　）
A．2B．4C．5D．$\frac{5}{2}$

分析 数列{an}满足anan+1=2n，可得：2=$\frac{{a}_{n+2}}{{a}_{n}}$．即可得出．

解答 解：∵数列{an}满足anan+1=2n，
∴$\frac{{a}_{n+1}{a}_{n+2}}{{a}_{n}{a}_{n+1}}$=$\frac{{2}^{n+1}}{{2}^{n}}$=2=$\frac{{a}_{n+2}}{{a}_{n}}$．
∴$\frac{{a}_{5}}{{a}_{3}}$=2，$\frac{{a}_{7}}{{a}_{5}}$=2，
则$\frac{{a}_{7}}{{a}_{3}}$=4．
故选：B．

点评 本题考查了数列的递推关系，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
20．y求下列函数的单调区间：y=2-cosx．
1．已知函数f（x）=|2x-1|+|x+1|-a的图象与x轴有且仅有一个交点．
（1）求实数a的值；
（2）若m，n∈[-a，a]，求证：2|m+n|＜|4+mn|
18．若480°角的终边上有一点（a，4），则a的值是（　　）
A．$\frac{4\sqrt{3}}{3}$B．$-\frac{4\sqrt{3}}{3}$C．4$\sqrt{3}$D．$-4\sqrt{3}$
5．已知函数f（x）的导函数f′（x），且瞒足f（x）=2xf′（1）+x3，则f′（1）等于（　　）
A．-1B．-3C．1D．3
15．已知函数f（x）=$\frac{\sqrt{2}}{2}$cos（2x+$\frac{π}{4}$）．
（1）若0＜α＜$\frac{π}{2}$，且cosα=$\frac{\sqrt{2}}{2}$，求f（α）的值；
（2）求函数f（x）的最小正周期及单调递增区间．
2．计算：$\frac{tan68°+tan52°}{1-tan68°tan52°}$=$-\sqrt{3}$．
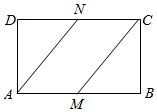15．如图在长方形ABCD中，$\overrightarrow{AB}=\overrightarrow a，\overrightarrow{AD}=\overrightarrow b，N$是CD的中点，M是线段AB上的点，$|{\overrightarrow a}|=2，|{\overrightarrow b}|=1$．
（1）若M是AB的中点，求证：$\overrightarrow{AN}$与$\overrightarrow{CM}$共线；
（2）在线段AB上是否存在点M，使得$\overrightarrow{BD}$与$\overrightarrow{CM}$垂直？若不存在请说明理由，若存在请求出M点的位置；
（3）若动点P在长方形ABCD上运动，试求$\overrightarrow{AP}•\overrightarrow{AB}$的最大值及取得最大值时P点的位置．
16．在等差数列{an}中，已知a4+a7=16，则该数列前11项和S11=（　　）
A．58B．88C．143D．176

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网