题目内容
9．矩形ABCD中，A（-1，3），B（-2，4），两条对角线交点在x轴上，则C点坐标为（-9，-3），D点坐标为（-8，-4）．分析 设M（x，0）为矩形对角线的交点，则|MA|=|MB|，利用两点之间的距离公式可得x，再利用中点坐标公式即可得出．
解答 解：设M（x，0）为矩形对角线的交点，则|MA|=|MB|，
∴$\sqrt{{（x+1）}^{2}+9}$=$\sqrt{{（x+2）}^{2}+16}$，
解得x=-5．
∴$\left\{\begin{array}{l}{-5=\frac{{x}_{c}-1}{2}}\\{0=\frac{{y}_{c}+3}{2}}\end{array}\right.$，解得C（-9，-3）．
同理可得D（-8，-4），
故答案为：（-9，-3），（-8，-4）．
点评 本题考查了两点之间的距离公式、中点坐标公式、矩形的性质，属于基础题．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
19．若方程$\frac{{x}^{2}}{3-m}$+$\frac{{y}^{2}}{m-1}$=1表示焦点在y轴上的椭圆，则实数m的取值范围为（ ）
| A． | （-∞，1） | B． | （1，2） | C． | （2，3） | D． | （3，+∞） |
4．若角α是三角形的内角，角α的正弦线、余弦线的长度相等，且正弦、余弦符号相异，那么角α=（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{π}{3}$ | C． | $\frac{3π}{4}$ | D． | $\frac{π}{4}$或$\frac{3π}{4}$ |
18．若480°角的终边上有一点（a，4），则a的值是（ ）
| A． | $\frac{4\sqrt{3}}{3}$ | B． | $-\frac{4\sqrt{3}}{3}$ | C． | 4$\sqrt{3}$ | D． | $-4\sqrt{3}$ |
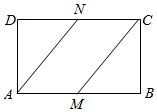如图在长方形ABCD中，$\overrightarrow{AB}=\overrightarrow a，\overrightarrow{AD}=\overrightarrow b，N$是CD的中点，M是线段AB上的点，$|{\overrightarrow a}|=2，|{\overrightarrow b}|=1$．