题目内容
3．
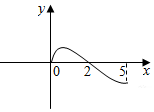奇函数f（x）的定义域为（-5，5），若x∈[0，5）时，f（x）的图象如图所示，则不等式f（x）＜0的解集为（-2，0）∪（2，5）．
分析 由奇函数的图象关于原点对称便可得出f（x）在（-5，0]上的图象，这样根据f（x）在（-5，5）上的图象便可得出f（x）＜0的解集．
解答 解：根据奇函数的图象关于原点对称得出f（x）在（-5，0]上的图象如下所示：
∴f（x）＜0的解集为（-2，0）∪（2，5）．
故答案为：（-2，0）∪（2，5）．
点评 考查奇函数的概念，奇函数图象的对称性，由函数图象解不等式f（x）＜0的方法．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
18．f（x）=$\frac{1}{2}$+$\frac{1}{{2}^{x}-1}$是（ ）
| A． | 奇函数 | B． | 偶函数 | ||
| C． | 是奇函数又是偶函数 | D． | 非奇函数非偶函数 |
14．已知实数x，y满足不等式组$\left\{\begin{array}{l}{lo{g}_{0.5}（2x-y）≥0}\\{1≤x≤2}\end{array}\right.$，z=x+2y，则（ ）
| A． | z的最大值为10，无最小值 | B． | z的最小值为3，无最大值 | ||
| C． | z的最大值为10，最小值为3 | D． | z的最大值为10，最小值为3 |
11．已知集合U={x∈Z|x2-x-12≤0}，A={-2，-1，3}，B={0，1，3，4}，则（∁∪A）∩B=（ ）
| A． | {0，2，4} | B． | {0，1，4} | C． | {0，4} | D． | {1，3} |
8．已知i是虚数单位，若z（1+i）=|i+1|，则z的虚部为（ ）
| A． | $\frac{{\sqrt{2}}}{2}$ | B． | $\frac{{-\sqrt{2}}}{2}$ | C． | $-\frac{{\sqrt{2}}}{2}i$ | D． | $\frac{{\sqrt{2}}}{2}i$ |
12．已知函数f（x）=x3+ax2+bx+c是定义在[2b-5，2b-3]上的奇函数，则$f（\frac{1}{2}）$的值为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{9}{8}$ | C． | 1 | D． | 无法确定 |