题目内容
12.已知函数f(x)=x3+ax2+bx+c是定义在[2b-5,2b-3]上的奇函数,则$f(\frac{1}{2})$的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{9}{8}$ | C. | 1 | D. | 无法确定 |
分析 根据奇函数的定义域关于原点对称,从而得出b=2,这样便可得出f(x)为定义在[-1,1]上的奇函数,从而得出f(0)=c=0,且有f(-1)=-f(1),这样便可得出a=0,从而得到f(x)=x3+2x,这样即可求出$f(\frac{1}{2})$的值.
解答 解:奇函数定义域关于原点对称;
∴2b-5=-(2b-3);
∴b=2;
∴f(x)是定义在[-1,1]上的奇函数;
∴f(0)=c=0;
∴f(-1)=-f(1);
即-1+a-2=-(1+a+2);
∴a=0;
∴f(x)=x3+2x;
∴$f(\frac{1}{2})=\frac{1}{8}+1=\frac{9}{8}$.
故选:B.
点评 考查奇函数的定义,奇函数定义域的对称性,奇函数在原点有定义时,原点处的函数值为0,以及已知函数求值的方法.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
20.圆(x-1)2+y2=1与圆x2+(y-1)2=2的位置关系为( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
1.幂函数y=x-2的大致图象是( )
| A. |  | B. |  | C. |  | D. |  |
2.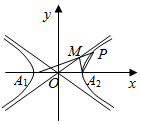 设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的顶点为A1,A2,P为双曲线上一点,直线PA1交双曲线C的一条渐近线于M点,直线A2M和A2P的斜率分别为k1,k2,若A2M⊥PA1且k1+4k2=0,则双曲线C离心率为( )
设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的顶点为A1,A2,P为双曲线上一点,直线PA1交双曲线C的一条渐近线于M点,直线A2M和A2P的斜率分别为k1,k2,若A2M⊥PA1且k1+4k2=0,则双曲线C离心率为( )
 设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的顶点为A1,A2,P为双曲线上一点,直线PA1交双曲线C的一条渐近线于M点,直线A2M和A2P的斜率分别为k1,k2,若A2M⊥PA1且k1+4k2=0,则双曲线C离心率为( )
设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的顶点为A1,A2,P为双曲线上一点,直线PA1交双曲线C的一条渐近线于M点,直线A2M和A2P的斜率分别为k1,k2,若A2M⊥PA1且k1+4k2=0,则双曲线C离心率为( )| A. | 2 | B. | $\frac{\sqrt{5}}{2}$ | C. | $\sqrt{5}$ | D. | 4 |
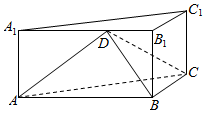 如图,在三棱柱ABC-A1B1C1中,BB1⊥平面ABC,∠ABC=90°,AB=2,BC=BB1=1,D是棱A1B1上一点.
如图,在三棱柱ABC-A1B1C1中,BB1⊥平面ABC,∠ABC=90°,AB=2,BC=BB1=1,D是棱A1B1上一点.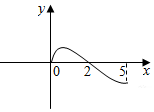 奇函数f(x)的定义域为(-5,5),若x∈[0,5)时,f(x)的图象如图所示,则不等式f(x)<0的解集为(-2,0)∪(2,5).
奇函数f(x)的定义域为(-5,5),若x∈[0,5)时,f(x)的图象如图所示,则不等式f(x)<0的解集为(-2,0)∪(2,5).