题目内容
11.已知集合U={x∈Z|x2-x-12≤0},A={-2,-1,3},B={0,1,3,4},则(∁∪A)∩B=( )| A. | {0,2,4} | B. | {0,1,4} | C. | {0,4} | D. | {1,3} |
分析 确定全集的元素,然后利用补集和交集,进行交补运算.
解答 解:集合U={x∈Z|x2-x-12≤0}={x∈Z|-3≤x≤4}={-3,-2,-1,0,1,2,3,4},A={-2,-1,3},
∴∁∪A={-3,0,1,2,4},
∵B={0,1,3,4},
∴(∁∪A)∩B={0,1,4},
故选:B.
点评 本题的考点是集合的交集和补集运算.先将集合进行化简是解决本题的关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案
相关题目
19.执行如图的程序框图,则输出S的值为( )


| A. | $\frac{199}{200}$ | B. | $\frac{197}{198}$ | C. | $\frac{197}{199}$ | D. | $\frac{198}{199}$ |
6.设等差数列{an}的前n项和为Sn,若数列{an}是单调递增数列,且满足a5≤6,S3≥9,则a6的取值范围是( )
| A. | (3,6] | B. | (3,6) | C. | [3,7] | D. | (3,7] |
16.复数z满足z•i=3+4i,则z在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.圆(x-1)2+y2=1与圆x2+(y-1)2=2的位置关系为( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
1.幂函数y=x-2的大致图象是( )
| A. |  | B. |  | C. |  | D. |  |
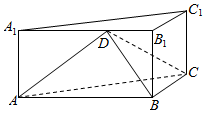 如图,在三棱柱ABC-A1B1C1中,BB1⊥平面ABC,∠ABC=90°,AB=2,BC=BB1=1,D是棱A1B1上一点.
如图,在三棱柱ABC-A1B1C1中,BB1⊥平面ABC,∠ABC=90°,AB=2,BC=BB1=1,D是棱A1B1上一点.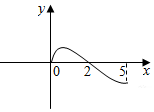 奇函数f(x)的定义域为(-5,5),若x∈[0,5)时,f(x)的图象如图所示,则不等式f(x)<0的解集为(-2,0)∪(2,5).
奇函数f(x)的定义域为(-5,5),若x∈[0,5)时,f(x)的图象如图所示,则不等式f(x)<0的解集为(-2,0)∪(2,5).