题目内容
18.△ABC的内角A,B,C所对的边分别为a,b,c,已知4sin2$\frac{A+B}{2}-cos2C=\frac{7}{2}$.(Ⅰ)求角C的大小;
(Ⅱ)若c=$\frac{{\sqrt{3}}}{2}$,求a-b的取值范围.
分析 (I)使用三角形的内角和公式和二倍角公式化简式子,得出关于cosC的方程;
(II)根据正弦定理得出a-b=sinA-sinB,消去B,得到关于A的三角函数,利用正弦函数的性质和A的范围求出.
解答 解:(Ⅰ)在△ABC中,A+B+C=π,
∴sin2$\frac{A+B}{2}$=$\frac{1-cos(A+B)}{2}$=$\frac{1+cosC}{2}$.
∵4sin2$\frac{A+B}{2}-cos2C=\frac{7}{2}$,
∴2(1+cosC)-(2cos2C-1)=$\frac{7}{2}$,即4cos2C-4cosC+1=0,
解得cosC=$\frac{1}{2}$.
∵C∈(0,π),∴C=$\frac{π}{3}$.
(Ⅱ)由正弦定理:$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=1$,
∵a-b=sinA-sinB=sinA-sin($\frac{2π}{3}-A$)=$\frac{1}{2}$sinA-$\frac{\sqrt{3}}{2}$cosA=sin(A-$\frac{π}{3}$).
∵A∈(0,$\frac{2π}{3}$),∴A-$\frac{π}{3}$∈(-$\frac{π}{3}$,$\frac{π}{3}$).
∴sin(A-$\frac{π}{3}$)<sin$\frac{π}{3}$=$\frac{\sqrt{3}}{2}$,
sin(A-$\frac{π}{3}$)>sin(-$\frac{π}{3}$)=-$\frac{\sqrt{3}}{2}$.
∴a-b的取值范围是(-$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$).
点评 本题考查了三角函数的恒等变换,正弦定理,正弦函数的图象与性质,属于中档题.

| A. | a+b+$\frac{1}{\sqrt{ab}}$>2$\sqrt{2}$ | B. | (a+b)($\frac{1}{a}$+$\frac{1}{b}$)>4 | ||
| C. | $\frac{{a}^{2}+{b}^{2}}{\sqrt{ab}}$>ab | D. | $\frac{2ab}{a+b}$>$\sqrt{ab}$ | ||
| E. | a+b+$\frac{1}{\sqrt{ab}}$>2$\sqrt{2}$ | F. | $\frac{{a}^{2}+{b}^{2}}{\sqrt{ab}}$≥$\frac{2ab}{\sqrt{ab}}$=$2\sqrt{ab}$ |
| A. | (-$\frac{5}{3}$,+∞) | B. | ($\frac{4}{3}$,+∞) | C. | (-∞,-$\frac{1}{3}$)∪($\frac{4}{3}$,+∞) | D. | (-$\frac{1}{3}$,+∞) |
| A. | (3,6] | B. | (3,6) | C. | [3,7] | D. | (3,7] |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $\frac{\sqrt{2}}{9}$ | B. | $\frac{2\sqrt{2}}{9}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{4\sqrt{2}}{9}$ |
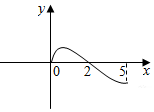 奇函数f(x)的定义域为(-5,5),若x∈[0,5)时,f(x)的图象如图所示,则不等式f(x)<0的解集为(-2,0)∪(2,5).
奇函数f(x)的定义域为(-5,5),若x∈[0,5)时,f(x)的图象如图所示,则不等式f(x)<0的解集为(-2,0)∪(2,5).