题目内容
8.已知i是虚数单位,若z(1+i)=|i+1|,则z的虚部为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{-\sqrt{2}}}{2}$ | C. | $-\frac{{\sqrt{2}}}{2}i$ | D. | $\frac{{\sqrt{2}}}{2}i$ |
分析 利用复数的运算法则、模的计算公式、虚部定义即可得出.
解答 解:z(1+i)=|i+1|,∴z=$\frac{\sqrt{2}}{1+i}$=$\frac{\sqrt{2}(1-i)}{(1+i)(1-i)}$=$\frac{\sqrt{2}}{2}$(1-i)=$\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i$,
则z的虚部为-$\frac{\sqrt{2}}{2}$.
故选:B.
点评 本题考查了复数的运算法则、模的计算公式、虚部定义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
19.执行如图的程序框图,则输出S的值为( )


| A. | $\frac{199}{200}$ | B. | $\frac{197}{198}$ | C. | $\frac{197}{199}$ | D. | $\frac{198}{199}$ |
16.复数z满足z•i=3+4i,则z在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.如果函数y=2sin(2x-φ)的图象关于点($\frac{4π}{3}$,0)中心对称,那么|φ|的最小值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
20.圆(x-1)2+y2=1与圆x2+(y-1)2=2的位置关系为( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
18.如图,在正六边形ABCDEF中,|$\overrightarrow{AC}$|=2$\sqrt{3}$,则$\overrightarrow{AF}$•$\overrightarrow{FB}$等于( )


| A. | -6 | B. | 6 | C. | -2$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
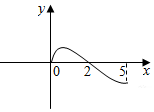 奇函数f(x)的定义域为(-5,5),若x∈[0,5)时,f(x)的图象如图所示,则不等式f(x)<0的解集为(-2,0)∪(2,5).
奇函数f(x)的定义域为(-5,5),若x∈[0,5)时,f(x)的图象如图所示,则不等式f(x)<0的解集为(-2,0)∪(2,5).