题目内容
13.若x(1-2x)4=a1x+a2x2+a3x3+a4x4+a5x5,则a2+a3+a4+a5=0.分析 x(1-2x)4=a1x+a2x2+a3x3+a4x4+a5x5,令x=1,可得:1=a1+a2+a3+a4+a5,另一方面:x(1-2x)4的一次项的系数为1.可得a1.即可得出.
解答 解:∵x(1-2x)4=a1x+a2x2+a3x3+a4x4+a5x5,
令x=1,则1×(1-2)4=1=a1+a2+a3+a4+a5,
另一方面:x(1-2x)4的一次项的系数为1×1=1.
∴a1=1.
则a2+a3+a4+a5=1-1=0.
故答案为:0.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.幂函数y=x-2的大致图象是( )
| A. |  | B. |  | C. |  | D. |  |
8.在三棱锥P-ABC中,底面ABC是等腰三角形,∠BAC=120°,BC=2,PA⊥平面ABC,若三棱锥P-ABC的外接球的表面积为8π,则该三棱锥的体积为( )
| A. | $\frac{\sqrt{2}}{9}$ | B. | $\frac{2\sqrt{2}}{9}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{4\sqrt{2}}{9}$ |
18.如图,在正六边形ABCDEF中,|$\overrightarrow{AC}$|=2$\sqrt{3}$,则$\overrightarrow{AF}$•$\overrightarrow{FB}$等于( )


| A. | -6 | B. | 6 | C. | -2$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
2.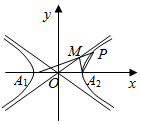 设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的顶点为A1,A2,P为双曲线上一点,直线PA1交双曲线C的一条渐近线于M点,直线A2M和A2P的斜率分别为k1,k2,若A2M⊥PA1且k1+4k2=0,则双曲线C离心率为( )
设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的顶点为A1,A2,P为双曲线上一点,直线PA1交双曲线C的一条渐近线于M点,直线A2M和A2P的斜率分别为k1,k2,若A2M⊥PA1且k1+4k2=0,则双曲线C离心率为( )
 设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的顶点为A1,A2,P为双曲线上一点,直线PA1交双曲线C的一条渐近线于M点,直线A2M和A2P的斜率分别为k1,k2,若A2M⊥PA1且k1+4k2=0,则双曲线C离心率为( )
设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的顶点为A1,A2,P为双曲线上一点,直线PA1交双曲线C的一条渐近线于M点,直线A2M和A2P的斜率分别为k1,k2,若A2M⊥PA1且k1+4k2=0,则双曲线C离心率为( )| A. | 2 | B. | $\frac{\sqrt{5}}{2}$ | C. | $\sqrt{5}$ | D. | 4 |
3.以双曲线$\frac{x^2}{9}-\frac{y^2}{16}$=1的焦点为顶点,顶点为焦点的椭圆方程是( )
| A. | $\frac{x^2}{16}+\frac{y^2}{9}$=1 | B. | $\frac{x^2}{25}+\frac{y^2}{16}$=1 | C. | $\frac{x^2}{25}+\frac{y^2}{9}$=1 | D. | $\frac{x^2}{16}+\frac{y^2}{25}$=1 |
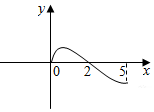 奇函数f(x)的定义域为(-5,5),若x∈[0,5)时,f(x)的图象如图所示,则不等式f(x)<0的解集为(-2,0)∪(2,5).
奇函数f(x)的定义域为(-5,5),若x∈[0,5)时,f(x)的图象如图所示,则不等式f(x)<0的解集为(-2,0)∪(2,5).