题目内容
 在正四棱锥S-ABCD中,SA=
在正四棱锥S-ABCD中,SA=| 2 |
| 3 |
(1)求证:EF∥平面SAB;
(2)求异面直线EF与SC所成角.
考点:直线与平面平行的判定,异面直线及其所成的角
专题:空间位置关系与距离
分析:(1)先作出辅助线,由面面平行得到线面平行,(2)先找到所求角为∠EFP,根据余弦定理求出即可.
解答:
解:如图所示:
作GF∥CD,FH∥SA,FP∥SC,连接EH,EF,
(1)∵GF∥AB,GE∥SB,
∴面SAB∥面GEF
∵EF∈面GEF
∴EF∥面SAB
(2)∵FP∥SC
∴所求角为∠EFP
在△EFP中,易求得EF=
,FP=
,EP=
根据余弦定理解得cosEFP=
,
∴∠EFP=30°
∴异面直线EF与SC所成的角为30°.
作GF∥CD,FH∥SA,FP∥SC,连接EH,EF,

(1)∵GF∥AB,GE∥SB,
∴面SAB∥面GEF
∵EF∈面GEF
∴EF∥面SAB
(2)∵FP∥SC
∴所求角为∠EFP
在△EFP中,易求得EF=
| 2 |
| ||
| 2 |
| ||
| 2 |
根据余弦定理解得cosEFP=
| 1 |
| 2 |
∴∠EFP=30°
∴异面直线EF与SC所成的角为30°.
点评:本题考查了线面平行的判定,考查了异面直线所成的角,是一道中档题.

练习册系列答案
相关题目
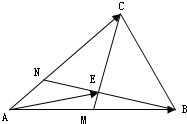 如图所示,在△ABC中,点M是AB的中点,且
如图所示,在△ABC中,点M是AB的中点,且