题目内容
函数f(x)=lg(||x2-2x-10|-10|)的零点的个数( )
| A、8 | B、7 | C、6 | D、5 |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:根据函数零点的定义.得到函数f(x)=lg(||x2-2x-10|-10|)的零点的个数即关x的方程||x2-2x-10|-10|=1的根的个数;将绝对值去掉,转化为二次方程根个数的判定.
解答:
解:函数f(x)=lg(||x2-2x-10|-10|)的零点的个数即
关x的方程||x2-2x-10|-10|=1的根的个数;
∴|x2-2x-10|-10=±1
∴|x2-2x-10|=11或|x2-2x-10|=9
∴x2-2x-10=±11或x2-2x-10=±9
∴x2-2x-21=0或x2-2x+1=0或x2-2x-19=0或x2-2x-1=0
∵△1=4+84=85>0
∴x2-2x-21=0有两个不相等的实根;
∵△2=4-4=0
∴x2-2x=1=0有两个相等的实根;
∵△3=4+76=80>0
∴x2-2x-19=0有两个不相等的实根;
∵△4=4+4=8>0
∴x2-2x-1=0有两个不相等的实根;
总之,关x的方程||x2-2x-10|-10|=1的根的个数为7,
故选B.
关x的方程||x2-2x-10|-10|=1的根的个数;
∴|x2-2x-10|-10=±1
∴|x2-2x-10|=11或|x2-2x-10|=9
∴x2-2x-10=±11或x2-2x-10=±9
∴x2-2x-21=0或x2-2x+1=0或x2-2x-19=0或x2-2x-1=0
∵△1=4+84=85>0
∴x2-2x-21=0有两个不相等的实根;
∵△2=4-4=0
∴x2-2x=1=0有两个相等的实根;
∵△3=4+76=80>0
∴x2-2x-19=0有两个不相等的实根;
∵△4=4+4=8>0
∴x2-2x-1=0有两个不相等的实根;
总之,关x的方程||x2-2x-10|-10|=1的根的个数为7,
故选B.
点评:本题主要考查函数的零点的定义,二次方程根个数的判定,求函数的零点,属于基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
如图是一个空间几何体的三视图,则这个几何体的侧面积是( )
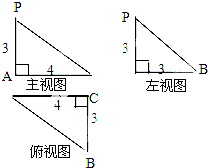

| A、42 | B、21 | C、24 | D、6 |
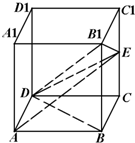 在棱长为2的正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.
在棱长为2的正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.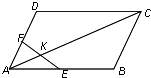 如图,一直线EF与平行四边形ABCD的两边AB,AD分别交于E、F两点,且交其对角线于K,其中,
如图,一直线EF与平行四边形ABCD的两边AB,AD分别交于E、F两点,且交其对角线于K,其中,