题目内容
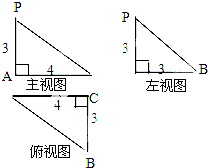
如图是一个空间几何体的三视图,则这个几何体的侧面积是( )

| A、42 | B、21 | C、24 | D、6 |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由三视图可知:原几何体是一个三棱锥,其中PA⊥平面ABC.AC⊥CB,PA=3,AC=4,BC=3.利用直角三角形的面积计算公式即可得出.
解答:
解:由三视图可知:原几何体是一个三棱锥, 其中PA⊥平面ABC.
其中PA⊥平面ABC.
AC⊥CB,PA=3,AC=4,BC=3.
∴这个几何体的侧面积=
×3×4+
×5×3+
×3×5
=21.
故选:B.
 其中PA⊥平面ABC.
其中PA⊥平面ABC.AC⊥CB,PA=3,AC=4,BC=3.
∴这个几何体的侧面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=21.
故选:B.
点评:本题考查了由三视图恢复原几何题、三棱锥的侧面积计算公式,属于基础题.

练习册系列答案
相关题目
函数f(x)=lg(||x2-2x-10|-10|)的零点的个数( )
| A、8 | B、7 | C、6 | D、5 |
钝角△ABC最大边长为4,其余两边长为x,y,以(x,y)为坐标的点所表示的平面区域的面积为( )
| A、4π-8 | ||
| B、4π+8 | ||
| C、4π-6 | ||
D、4π-
|
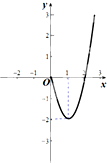 已知定义在R上奇函数f(x)在x≥0时的图象是如图所示的抛物线的一部分.
已知定义在R上奇函数f(x)在x≥0时的图象是如图所示的抛物线的一部分.