题目内容
19.已知点A(-1,0),B(1,0),C(0,1),直线y=kx+b(k≥0)将△ABC分割为面积相等的两部分,则b的取值范围是( )| A. | (0,1) | B. | $[\frac{1}{3},\frac{1}{2})$ | C. | $[1-\frac{{\sqrt{2}}}{2},\frac{1}{3}]$ | D. | $[1-\frac{{\sqrt{2}}}{2},\frac{1}{2})$ |
分析 考查临界位置时对应的b值,综合可得结论.
解答  解:k=0时,y=b,$(1-b)^{2}=\frac{1}{2}$,∴b=1-$\frac{\sqrt{2}}{2}$;
解:k=0时,y=b,$(1-b)^{2}=\frac{1}{2}$,∴b=1-$\frac{\sqrt{2}}{2}$;
k>0时,如右上图,$N(-\frac{b}{k},0),{y_M}=\frac{k+b}{k+1}$
令${S_{△MNB}}=\frac{1}{2}(1+\frac{b}{k})•\frac{k+b}{k+1}=\frac{1}{2}$,得$k=\frac{b^2}{1-2b}>0∴b<\frac{1}{2}$,
故选D.
点评 本题主要考查确定直线的要素,点到直线的距离公式以及三角形的面积公式的应用,还考察运算能力以及综合分析能力,分类讨论思想,属于中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
4.设x=3+4i,则复数z=x-|x|-(1-i) 的虚部为( )
| A. | 3 | B. | -3+5i | C. | 5i | D. | 5 |
11.下列命题正确的是( )
| A. | 若a>b,则ac2>bc2 | B. | 若a>b>0,c>d>0,则$\frac{a}{d}>\frac{b}{c}$ | ||
| C. | 若a<b<0,则ab<b2 | D. | 若$\frac{a}{b}>1$,则a>b |
 如图所示,直三棱柱ABC-A1B1C1中,AC=3,AB=BB1=4,BC=5,D为BC的中点.
如图所示,直三棱柱ABC-A1B1C1中,AC=3,AB=BB1=4,BC=5,D为BC的中点.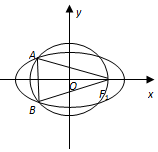 如图,F1是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点,A和B是以O为圆心,以|OF1|为半径的圆与该左半椭圆的两个交点,且△F1AB是等边三角形,求椭圆的离心率.
如图,F1是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点,A和B是以O为圆心,以|OF1|为半径的圆与该左半椭圆的两个交点,且△F1AB是等边三角形,求椭圆的离心率.