题目内容
4.设x=3+4i,则复数z=x-|x|-(1-i) 的虚部为( )| A. | 3 | B. | -3+5i | C. | 5i | D. | 5 |
分析 由已知求出|x|,代入z=x-|x|-(1-i)化简得答案.
解答 解:∵x=3+4i,
∴|x|=$\sqrt{{3}^{2}+{4}^{2}}=5$,
∴z=x-|x|-(1-i)=3+4i-5-1+i=-3+5i.
∴复数z=x-|x|-(1-i) 的虚部为5.
故选:D.
点评 本题考查复数代数形式的乘除运算,考查复数模的求法,是基础的计算题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.将一块边长为10的正方形铁片按图1所示的阴影部分裁下,用余下的四个全等的等腰三角形加工成一个底面边长为x的正四棱锥形容器(如图2),则函数f(x)=$\frac{{V}_{E-ABCD}}{x}$的最大值为( )
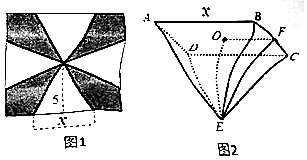

| A. | $\frac{25\sqrt{3}}{6}$ | B. | $\frac{50}{3}$ | C. | $\frac{25}{3}$ | D. | $\frac{125\sqrt{3}}{6}$ |
19.已知点A(-1,0),B(1,0),C(0,1),直线y=kx+b(k≥0)将△ABC分割为面积相等的两部分,则b的取值范围是( )
| A. | (0,1) | B. | $[\frac{1}{3},\frac{1}{2})$ | C. | $[1-\frac{{\sqrt{2}}}{2},\frac{1}{3}]$ | D. | $[1-\frac{{\sqrt{2}}}{2},\frac{1}{2})$ |
16.设等差数列{an}的前n项和为Sn,若S3=3,S6=15,则a10+a11+a12=( )
| A. | 21 | B. | 30 | C. | 12 | D. | 39 |