题目内容
3．
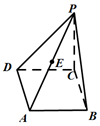如图在边长为2的菱形ABCD中，∠ABC=60°，PC⊥平面ABCD，PC=2，E为PA的中点．（1）求证：平面EBD⊥平面ABCD；
（2）求点E到平面PBC的距离．
分析 （1）连结DB，AC交于点O，证明OE∥PC，可得OE⊥平面ABCD，可证平面EBD⊥平面ABCD．
（2）过A作AH⊥BC于H，点A到面PBC的距离等于线段AH的长，点E到平面PBC的距离为AH的一半．
解答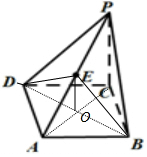 
解：（1）连结DB，AC交于点O，
因为四边形ABCD为菱形，∴O为AC中点，即OE∥PC，
∵PC⊥平面ABCD，∴OE⊥平面ABCD
∵OE?面DBE，∴平面EBD⊥平面ABCD
（2）过A作AH⊥BC于H，∵PC⊥平面ABCD，∴AN⊥面PBC，
点A到面PBC的距离等于线段AH的长，
∵菱形ABCD的边长为2，∠ABC=60°，∴AH=$\sqrt{3}$
∵E为PA的中点，∴点E到平面PBC的距离为$\frac{\sqrt{3}}{2}$
点评 本题考查了空间线面位置关系，点面距离，属于中档题．
练习册系列答案
相关题目
11．如果函数f（x）=3cos（2x+$\frac{π}{6}$），则f（x）的图象（ ）
| A． | 关于点（-$\frac{π}{12}$，0）对称 | B． | 关于点（$\frac{π}{6}$，0）对称 | ||
| C． | 关于直线x=$\frac{π}{6}$对称 | D． | 关于直线x=$\frac{π}{2}$对称 |
8．如图是正方体的侧面展开图，l1、l2是两条侧面对角线，则在此正方体中，l1与l2（ ）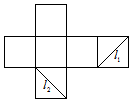
| A． | 互相平行 | B． | 相交且夹角为$\frac{π}{3}$ | C． | 异面且互相垂直 | D． | 异面且夹角为$\frac{π}{3}$ |