题目内容
8.已知在直角坐标系xOy中,直线l的参数方程为$\left\{\begin{array}{l}{x=t-2}\\{y=\sqrt{3}t}\end{array}\right.$(t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ2-4ρcosθ+3=0,设点P是曲线C上的一个动点,则P到直线l距离的取值范围是[2$\sqrt{3}$-1,2$\sqrt{3}$+1].分析 直接根据直线的参数方程中,消去参数,即可得到其普通方程;再利用极坐标方程和直角坐标方程互化公式求解即可,设点P(2+cosθ,sinθ)(θ∈R),然后,构造距离关系式,然后,求解其范围即可.
解答 解:根据$\left\{\begin{array}{l}{x=t-2}\\{y=\sqrt{3}t}\end{array}\right.$(t为参数),消去t,得直线l的普通方程为:$\sqrt{3}$x-y+2$\sqrt{3}$=0
依据曲线C的极坐标方程为ρ2-4ρcosθ+3=0.得到曲线的直角坐标方程为(x-2)2+y2=1
设点P(2+cosθ,sinθ)(θ∈R),
则d=$\frac{|\sqrt{3}(2+cosθ)-sinθ+2\sqrt{3}|}{2}$=$\frac{|2cos(θ+\frac{π}{6})+4\sqrt{3}|}{2}$
所以d的取值范围是[2$\sqrt{3}$-1,2$\sqrt{3}$+1].
故答案为[2$\sqrt{3}$-1,2$\sqrt{3}$+1].
点评 本题重点考查了参数方程和普通方程的互化、极坐标方程和直角坐标方程的互化等知识,属于中档题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
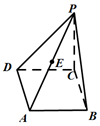 如图在边长为2的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,PC=2,E为PA的中点.
如图在边长为2的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,PC=2,E为PA的中点.