题目内容
18．经过点M（4，1）作直线l交双曲线${x^2}-\frac{y^2}{2}=1$于A、B两点，且M是AB的中点，则直线l的方程为y=8x-31．分析 设点A（x1，y1），点B（x2，y2），M（x0，y0），得到2x12-y12=2 ①，2x22-y22=2 ②然后，①-②并结合有关中点坐标公式求解．
解答 解：设点A（x1，y1），点B（x2，y2），M（x0，y0），
则2x12-y12=2 ①
2x22-y22=2 ②
①-②得2（x1+x2）（x1-x2）-（y1+y2）（y1-y2）=0，
∴16-2k=0，
∴k=8，
∴y-1=8（x-4），
∴直线l的方程为8x-y-31=0，
故答案为：8x-31．
点评 本题重点考查了直线与双曲线的位置关系、中点弦问题等知识，处理中点弦问题时，常常采用“点差法”进行处理．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
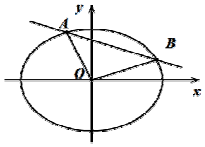已知椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，且过点$P（1，\frac{3}{2}）$，直线l：y=kx+m交椭圆E于不同的两点A，B，设线段AB的中点为M．
13．
如图，在长方体ABCD-A1B1C1D1中，AB=BC=2，AA1=1，则AC1与平面A1B1C1D1所成的角的正弦值为（ ）
如图，在长方体ABCD-A1B1C1D1中，AB=BC=2，AA1=1，则AC1与平面A1B1C1D1所成的角的正弦值为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{{2\sqrt{2}}}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{{\sqrt{2}}}{4}$ |
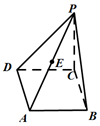如图在边长为2的菱形ABCD中，∠ABC=60°，PC⊥平面ABCD，PC=2，E为PA的中点．