题目内容
13.若函数f(x)=$\left\{\begin{array}{l}{{a}^{x},x>1}\\{(4-\frac{a}{2})x+2,x≤1}\end{array}\right.$的值域为R,则实数a的取值范围是(1,4].分析 f(x)是分段函数,在每一区间内求f(x)的取值范围,再求它们的并集得出值域;由f(x)的值域为R,得出a的取值范围.
解答 解:函数f(x)=$\left\{\begin{array}{l}{{a}^{x},x>1}\\{(4-\frac{a}{2})x+2,x≤1}\end{array}\right.$,
当8>a>1时,f(x)=ax,在(1,+∞)上为增函数,f(x)∈(a,+∞);
当x≤1时,f(x)=(4-$\frac{a}{2}$)x+2,在(-∞,1]上的值域,f(x)∈(-∞,6-$\frac{a}{2}$];
若f(x)的值域为R,则(-∞,6$-\frac{a}{2}$]∪(a,+∞)=R,
则6-$\frac{a}{2}$≥a,
即1<a≤4;
当a∈(0,1)时,指数函数是减函数,一次函数是增函数,值域不可能为R.
当a≥8时,指数函数是增函数,一次函数是减函数,函数的值域不可能为R.
则实数a的取值范围是(1,4].
故答案为:(1,4].
点评 本题考查了分段函数的值域问题和分类讨论的数学思想,分段函数的值域是在区间内求出函数的取值范围,再求它们的并集即得出值域.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
4.命题p:直线l与抛物线C有且仅有一个公共点;命题q:直线l与抛物线C相切.则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
1.过点(3,2)且与椭圆3x2+8y2=24有相同焦点的椭圆方程为( )
| A. | $\frac{x^2}{5}+\frac{y^2}{10}=1$ | B. | $\frac{x^2}{10}+\frac{y^2}{15}=1$ | C. | $\frac{x^2}{15}+\frac{y^2}{10}=1$ | D. | $\frac{x^2}{25}+\frac{y^2}{10}=1$ |
18.已知loga9=-2,则a的值为( )
| A. | -3 | B. | $-\frac{1}{3}$ | C. | 3 | D. | $\frac{1}{3}$ |
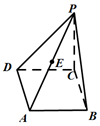 如图在边长为2的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,PC=2,E为PA的中点.
如图在边长为2的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,PC=2,E为PA的中点.