题目内容
11.如果函数f(x)=3cos(2x+$\frac{π}{6}$),则f(x)的图象( )| A. | 关于点(-$\frac{π}{12}$,0)对称 | B. | 关于点($\frac{π}{6}$,0)对称 | ||
| C. | 关于直线x=$\frac{π}{6}$对称 | D. | 关于直线x=$\frac{π}{2}$对称 |
分析 根据余弦函数f(x)的图象与性质,对选项中的命题进行分析、判断正误即可.
解答 解:函数f(x)=3cos(2x+$\frac{π}{6}$),则
f(-$\frac{π}{12}$)=3cos(-$\frac{π}{6}$+$\frac{π}{6}$)=3≠0,
∴f(x)的图象不关于点(-$\frac{π}{12}$,0)对称,A错误;
f($\frac{π}{6}$)=3cos($\frac{π}{3}$+$\frac{π}{6}$)=0,
∴f(x)的图象关于点($\frac{π}{6}$,0)对称,B正确;
∴f(x)的图象不关于直线x=$\frac{π}{6}$对称,C错误;
f($\frac{π}{2}$)=3cos(π+$\frac{π}{6}$)=-$\frac{3\sqrt{3}}{2}$,
∴f(x)的图象不关于直线x=$\frac{π}{2}$对称,D错误.
故选:B.
点评 本题考查了余弦函数f(x)的图象与性质的应用问题,是基础题.

练习册系列答案
相关题目
16.已知O为坐标原点,F为抛物线y2=2px(p>0)的焦点,若抛物线与直线l:x-$\sqrt{3}$y-$\frac{p}{2}$=0在第一、四象限分别交于A,B两点.则$\frac{(\overrightarrow{OF}-\overrightarrow{OA})^{2}}{(\overrightarrow{OF}-\overrightarrow{OB})^{2}}$的值等于( )
| A. | 97+56$\sqrt{3}$ | B. | 144 | C. | 73+40$\sqrt{3}$ | D. | 4p2 |
19.直线y=k(x-1)与A(3,2)、B(0,1)为端点的线段有公共点,则k的取值范围是( )
| A. | [-1,1] | B. | [-1,3] | C. | (-∞,-1]∪[3,+∞) | D. | (-∞,-1]∪[1,+∞) |
16.已知函数y=f(x)的定义在实数集R上的奇函数,且当x∈(-∞,0)时,xf'(x)<f(-x)(其中f'(x)是f(x)的导函数),若a=$\sqrt{3}$f($\sqrt{3})$,b=(lg3)f(lg3),c=$({log_3}\frac{1}{3})f({log_3}\frac{1}{3})$,则( )
| A. | c>a>b | B. | c>b>a | C. | a>b>c | D. | a>c>b |
1.过点(3,2)且与椭圆3x2+8y2=24有相同焦点的椭圆方程为( )
| A. | $\frac{x^2}{5}+\frac{y^2}{10}=1$ | B. | $\frac{x^2}{10}+\frac{y^2}{15}=1$ | C. | $\frac{x^2}{15}+\frac{y^2}{10}=1$ | D. | $\frac{x^2}{25}+\frac{y^2}{10}=1$ |
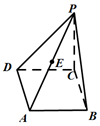 如图在边长为2的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,PC=2,E为PA的中点.
如图在边长为2的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,PC=2,E为PA的中点.