题目内容
14.已知函数$f(x)=\frac{{{2^x}-a}}{{{2^x}+a}}$是奇函数,其中a∈R,求a的值.分析 根据函数的奇偶得到(2-x-a)(2-x+a)(2x-a)=0,求出2(1-a2)=0,求出a的值即可.
解答 解:∵f(x)是奇函数,
∴由f(-x)=-f(x)得:$\frac{{2}^{-x}-a}{{2}^{-x}+a}$=-$\frac{{2}^{x}-a}{{2}^{x}+a}$,
故(2-x-a)(2-x+a)(2x-a)=0,
故2(1-a2)=0,解得:a=±1.
点评 本题考查了函数的奇偶性问题,是一道基础题.

练习册系列答案
相关题目
19.直线y=k(x-1)与A(3,2)、B(0,1)为端点的线段有公共点,则k的取值范围是( )
| A. | [-1,1] | B. | [-1,3] | C. | (-∞,-1]∪[3,+∞) | D. | (-∞,-1]∪[1,+∞) |
4.命题p:直线l与抛物线C有且仅有一个公共点;命题q:直线l与抛物线C相切.则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
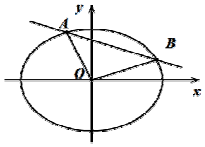 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,且过点$P(1,\frac{3}{2})$,直线l:y=kx+m交椭圆E于不同的两点A,B,设线段AB的中点为M.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,且过点$P(1,\frac{3}{2})$,直线l:y=kx+m交椭圆E于不同的两点A,B,设线段AB的中点为M.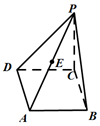 如图在边长为2的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,PC=2,E为PA的中点.
如图在边长为2的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,PC=2,E为PA的中点.