题目内容
15.已知命题$p:?{x_0}∈R,使x_0^2+{x_0}+1<0,命题q:?a∈R,若b>c,则ab>ac$,给出下列结论:①命题“p∧q”是真命题
②命题“p∨q”是真命题
③命题“(?p)∨q”是真命题
④命题“(?p)∧(?q)”是真命题
其中正确的是( )
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ③④ |
分析 运用配方法,可得p为假;取a=0,可得q为假.再由复合命题的真值表,可得①②错;③④真.
解答 解:命题$p:?{x_0}∈R,使x_0^2+{x_0}+1<0,命题q:?a∈R,若b>c,则ab>ac$,
由于x2+x+1=(x+$\frac{1}{2}$)2+$\frac{3}{4}$>0恒成立,可得p为假命题;
若a=0,则ab=ac,可得q为假命题.
则①命题“p∧q”是假命题,故①错;
②命题“p∨q”是假命题,故②错;
③命题“(?p)∨q”是真命题,故③真;
④命题“(?p)∧(?q)”是真命题,故④真.
故选:D.
点评 本题考查命题的真假判断,考查二次函数的性质和不等式的性质,考查复合命题的真值表,考查判断能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.命题p:直线l与抛物线C有且仅有一个公共点;命题q:直线l与抛物线C相切.则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
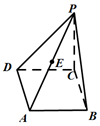 如图在边长为2的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,PC=2,E为PA的中点.
如图在边长为2的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,PC=2,E为PA的中点.