题目内容
12.已知a>0,函数f(x)=ax-x2.求f(x)≤1,x∈[0,1]恒成立的充要条件.分析 根据充要条件的定义,以及函数恒成立,即可求出a的范围.
解答 解:因为f(x)=ax-x2,当x=0时,f(x)=0≤1成立,
当x∈(0,1]时,f(x)≤1恒成立
即a≤x+$\frac{1}{x}$在(0,1]上恒成立,
又(x+$\frac{1}{x}$)min=2,此时x=1,
所以0<a≤2,
当0<a≤2时,a≤x+$\frac{1}{x}$在(0,1]上恒成立,所以f(x)≤1在(0,1]上恒成立,
所以f(x)≤1,x∈(0,1]上恒成立的充要条件为0<a≤2.
点评 本题主要考查了函数恒成立问题,以及分离讨论的数学思想,属于基础题.

练习册系列答案
相关题目
4.命题p:直线l与抛物线C有且仅有一个公共点;命题q:直线l与抛物线C相切.则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
1.过点(3,2)且与椭圆3x2+8y2=24有相同焦点的椭圆方程为( )
| A. | $\frac{x^2}{5}+\frac{y^2}{10}=1$ | B. | $\frac{x^2}{10}+\frac{y^2}{15}=1$ | C. | $\frac{x^2}{15}+\frac{y^2}{10}=1$ | D. | $\frac{x^2}{25}+\frac{y^2}{10}=1$ |
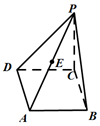 如图在边长为2的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,PC=2,E为PA的中点.
如图在边长为2的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,PC=2,E为PA的中点.