题目内容
已知函数f(x)=x2+1,且g(x)=f[f(x)],G(x)=g(x)-2af(x)
(1)若a=3,求函数G(x)的最小值;
(2)是否存在实数a使得G(x)在(-∞,-1)上为减函数,在(-1,0)为增函数?若存在,求出实数a的值,若不存在,请说明理由.
(1)若a=3,求函数G(x)的最小值;
(2)是否存在实数a使得G(x)在(-∞,-1)上为减函数,在(-1,0)为增函数?若存在,求出实数a的值,若不存在,请说明理由.
考点:函数单调性的判断与证明
专题:导数的综合应用
分析:由f(x)得到g(x),再由g(x)得到G(x),通过求导找到函数的单调区间,从而找到函数的最值.
解答:
解(1);∵函数f(x)=x2+1,
∴g(x)=f[f(x)]
=f(x2+1)=(x2+1)2+1
=x4+2x2+2,
当a=3时,
G(x)=g(x)-2af(x)
=x4-4x2-4,
∴G′(x)=4x3-8x,令G′(x)=0,解得:x=-1,x=0,x=1,
在(-∞,-1)上,G(x)递减,在(-1,0)上,G(x)递增,
∴G(-1)是极小值,G(-1)=-7;
在(0,1)上,G(x)递减,在(1,+∞)上,G(x)递增,
∴G(1)是极小值,G(1)=-7;
∴G(x)的最小值是-7.
(2)由(1)得:g(x)=x4+2x2+2,
∴G(x)=x4+2x2+2-2a(x2+1)
=x4+(2-2a)x2+(2-2a),
∴G′(-1)=0,解得;a=
,
∴存在a=
,使得G(x)在(-∞,-1)上为减函数,在(-1,0)为增函数.
∴g(x)=f[f(x)]
=f(x2+1)=(x2+1)2+1
=x4+2x2+2,
当a=3时,
G(x)=g(x)-2af(x)
=x4-4x2-4,
∴G′(x)=4x3-8x,令G′(x)=0,解得:x=-1,x=0,x=1,
在(-∞,-1)上,G(x)递减,在(-1,0)上,G(x)递增,
∴G(-1)是极小值,G(-1)=-7;
在(0,1)上,G(x)递减,在(1,+∞)上,G(x)递增,
∴G(1)是极小值,G(1)=-7;
∴G(x)的最小值是-7.
(2)由(1)得:g(x)=x4+2x2+2,
∴G(x)=x4+2x2+2-2a(x2+1)
=x4+(2-2a)x2+(2-2a),
∴G′(-1)=0,解得;a=
| 3 |
| 2 |
∴存在a=
| 3 |
| 2 |
点评:本题属于求函数的单调性及最值的问题,通过求导的方式解决.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列命题正确的是( )
| A、以直角三角形的一直角边为轴旋转所得的旋转体是圆锥 |
| B、以直角梯形的一腰为轴旋转所得的旋转体是圆台 |
| C、圆柱、圆锥、圆台都有两个底面 |
| D、圆锥的侧面展开图为扇形,此扇形所在圆的半径等于圆锥底面圆半径 |
已知i是虚数单位,若iz=1+2i,则
=( )
. |
| z |
| A、2+i | ||||
| B、2-i | ||||
C、
| ||||
D、
|
设a∈R,则“a=-1”是“直线ax+y-1=0与直线x+y+5=0垂直”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知sin(θ-
)=2cos(θ+
),则
=( )
| π |
| 4 |
| π |
| 4 |
sin(
| ||
sin(
|
| A、-4 | ||
| B、-2 | ||
C、
| ||
| D、-1 |
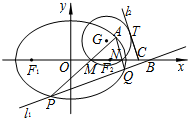 已知椭圆E:x2+2y2=6 的两个焦点为F1、F2,A是椭圆上位于第一象限的一点,△AF1F2的面积为
已知椭圆E:x2+2y2=6 的两个焦点为F1、F2,A是椭圆上位于第一象限的一点,△AF1F2的面积为