题目内容
设a∈R，则“a=-1”是“直线ax+y-1=0与直线x+y+5=0垂直”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：当a=1时两直线的斜率都存在，故只要看是否满足k1•k2=-1即可．利用直线的垂直求出a的值，然后判断充要条件即可．
解答：
解：当a=-1时直线ax+y-1=0的斜率是1，直线x+y+5=0的斜率是-1，
满足k1•k2=-1
∴a=-1时直线ax+y-1=0与直线x+y+5=0垂直，
直线ax+y-1=0与直线x+y+5=0垂直，则a+1=0，解得a=-1，
“a=1”是“直线ax+y-1=0与直线x+y+5=0垂直”的充分必要条件．
故选：C
满足k1•k2=-1
∴a=-1时直线ax+y-1=0与直线x+y+5=0垂直，
直线ax+y-1=0与直线x+y+5=0垂直，则a+1=0，解得a=-1，
“a=1”是“直线ax+y-1=0与直线x+y+5=0垂直”的充分必要条件．
故选：C
点评：本题考查的知识点是充要条件，熟练掌握充要条件的定义是解答的关键．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
相关题目
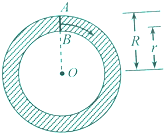如图，我们知道，圆环也可看作线段AB绕圆心O旋转一周所形成的平面图形，又圆环的面积S=π（R2-r2）=（R-r）×2π×| R+r |
| 2 |
| R+r |
| 2 |
| A、2πr2d |
| B、2π2r2d |
| C、2πrd2 |
| D、2π2rd2 |
（x-1）x=0是x=0的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
三角形ABC中，A，B，C的对边分别为a，b，c，已知下列条件：
①b=3，c=4，B=30°；
②a=5，b=8，A=30°；
③c=6，b=3
，B=60°；
④c=9，b=12，C=60°
其中满足上述条件的三角形有两解的是（ ）
①b=3，c=4，B=30°；
②a=5，b=8，A=30°；
③c=6，b=3
| 3 |
④c=9，b=12，C=60°
其中满足上述条件的三角形有两解的是（ ）
| A、①② | B、①④ | C、①②③ | D、③④ |
已知数列{an}，a1=
，an=1-
（n≥2），则a2014=（ ）
| 1 |
| 4 |
| 1 |
| an-1 |
A、
| ||
B、
| ||
| C、-3 | ||
D、
|
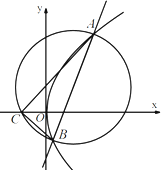已知抛物线的顶点为（0，0），准线为x=-2，不垂直于x轴的直线x=ty+1与该抛物线交于A，B两点，圆M以AB为直径．