题目内容
16.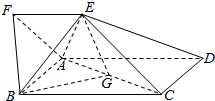 如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,且平面ABCD⊥平面ADEF,AF=FE=AB=$\frac{1}{2}AD$=2,点G为AC的中点.
如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,且平面ABCD⊥平面ADEF,AF=FE=AB=$\frac{1}{2}AD$=2,点G为AC的中点.(1)求证:EG∥平面ABF;
(2)求三棱锥B-AEG的体积.
分析 (1)取AB中点M,连FM,GM,证明EG∥FM.然后证明EG∥平面ABF.
(2)作EN⊥AD,垂足为N,说明EN为三棱锥E-ABG的高.利用等体积法,通过${V}_{B-AEG}={V}_{E-ABG}=\frac{1}{3}{S}_{△ABG}•EN$求解即可.
解答 (1)证明:取AB中点M,连FM,GM. …(1分)
∵G为对角线AC的中点,
∴GM∥AD,且GM=$\frac{1}{2}$AD,
又∵FE∥$\frac{1}{2}$AD,
∴GM∥FE且GM=FE.
∴四边形GMFE为平行四边形,即EG∥FM. …(4分)
又∵EG?平面ABF,FM?平面ABF,
∴EG∥平面ABF. …(6分)
(2)解:作EN⊥AD,垂足为N,
由平面ABCD⊥平面AFED,面ABCD∩面AFED=AD,
得EN⊥平面ABCD,即EN为三棱锥E-ABG的高.
∵在△AEF中,AF=FE,∠AFE=60°,
∴△AEF是正三角形.
∴∠AEF=60°,
由EF∥AD知∠EAD=60°,
∴EN=AE?sin60°=$\sqrt{3}$. …(10分)
∴三棱锥B-AEG的体积为${V_{B-AEG}}={V_{E-ABG}}=\frac{1}{3}{S_{△ABG}}•EN=\frac{1}{3}×\frac{1}{2}×2×2×\sqrt{3}=\frac{{2\sqrt{3}}}{3}$. …(13分)
点评 本题考查直线与平面平行的判定定理的应用,几何体的体积的求法,考查空间想象能力以及计算能力.转化思想的应用.

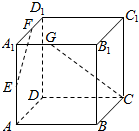 如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AA1,A1D1,A1B1的中点,则异面直线EF与CG所成的角等于( )
如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AA1,A1D1,A1B1的中点,则异面直线EF与CG所成的角等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
| A. | $\frac{1}{4}<m<1$ | B. | m>1 | C. | $m<\frac{1}{4}$ | D. | $m<\frac{1}{4}$或m>1 |
| A. | $\frac{3}{10}$ | B. | $\frac{3}{20}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |
| A. | 若x=1,则x2≠1 | B. | 若x≠1,则x2=1 | C. | 若x≠1,则x2≠1 | D. | 若x2≠1,则x≠1 |
