题目内容
19．某工厂接到一任务，需加工6000个P型零件和2000个Q型零件．这个厂有214名工人，他们每一个人用以加工5个P型零件的时间可以加工3个Q型零件，将这些工人分成两组同时工作，每组加工一种型号的零件．为了在最短时间内完成这批任务，则加工P型零件的人数为137人．分析 设最短加工时间为x，建立方程关系进行求解即可．
解答 解：设最短加工时间为x，
则加工P型零件的人数为$\frac{6000}{5x}$=$\frac{1200}{x}$，则加工Q型零件的人数为$\frac{2000}{3x}$，
则满足$\frac{1200}{x}$+$\frac{2000}{3x}$=214，
即$\frac{3600+2000}{3x}$=214，
即$\frac{5600}{3x}$=214，
则$\frac{1}{x}$=$\frac{642}{5600}$，
则加工P型零件的人数为$\frac{1200}{x}$=1200×$\frac{642}{5600}$=137.57，
故加工P型零件的人数为137人，
故答案为：137
点评 本题主要考查函数的应用问题，根据条件设出变量，建立方程关系是解决本题的关键．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
10．已知四边形ABCD是平行四边形，对角线相交于点O，则下列等式中成立的是（ ）
| A． | $\overrightarrow{BC}$+$\overrightarrow{BA}$=$\overrightarrow{AC}$ | B． | $\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{BC}$ | C． | $\overrightarrow{AO}$=$\frac{1}{2}$（$\overrightarrow{AB}$+$\overrightarrow{AD}$） | D． | $\overrightarrow{AD}$=$\overrightarrow{CB}$ |
7．
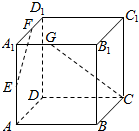如图，在正方体ABCD-A1B1C1D1中，E、F、G分别是AA1，A1D1，A1B1的中点，则异面直线EF与CG所成的角等于（ ）
如图，在正方体ABCD-A1B1C1D1中，E、F、G分别是AA1，A1D1，A1B1的中点，则异面直线EF与CG所成的角等于（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
某地区要建造一条防洪堤，其横断面为等腰梯形，腰与底边所成角为60°（如图所示），考虑到防洪堤的坚固性及石块用料等因素，设计其横断面要求面积为9$\sqrt{3}$m2，且髙度不低于$\sqrt{3}$m．问防洪堤横断面的腰长AB为多少时，横断面的外周长AB+BC+CD最小，并求最小外周长：