题目内容
5.设0<x<2,求函数y=$\sqrt{3x•(8-3x)}$的最大值.分析 根据题意,设t=3x(8-3x),结合二次函数的性质分析可得当x=$\frac{4}{3}$时,t=3x(8-3x)有最大值16,进而分析可得y=$\sqrt{3x•(8-3x)}$的最大值,即可得答案.
解答 解:根据题意,设t=3x(8-3x),0<x<2
则t=3x(8-3x)=-9x2+24x,(0<x<2)
分析可得当x=$\frac{4}{3}$时,t=3x(8-3x)有最大值16,
则此时y=$\sqrt{3x•(8-3x)}$有最大值$\sqrt{16}$=4;
故函数y=$\sqrt{3x•(8-3x)}$的最大值为4.
点评 本题考查函数最值的计算,关键是转化思路,利用二次函数的性质求出函数t=3x(8-3x)的最大值.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
13.若实数x、y满足约束条件$\left\{\begin{array}{l}{2x-y-2≤0}\\{2x+y-4≥0}\\{y≤2}\end{array}\right.$,则$\frac{x}{y}$的取值范围是( )
| A. | [$\frac{2}{3}$,2] | B. | [$\frac{1}{2}$,$\frac{3}{2}$] | C. | [$\frac{3}{2}$,2] | D. | [1,2] |
3.已知集合A={1,m2},B={0,4},则“m=-2”是“A∩B={4}”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
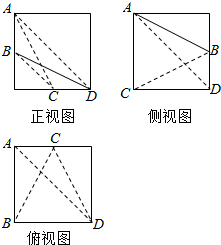 已知,棱长为2的正方体内有一内接四面体A-BCD,且B,C分别为正方体某两条棱的中点,其三视图如图所示:
已知,棱长为2的正方体内有一内接四面体A-BCD,且B,C分别为正方体某两条棱的中点,其三视图如图所示: