题目内容
有两只水桶,桶1中有a升水,桶2是空桶.现将桶1中的水缓慢注入桶2中,t分钟后桶1中剩余的水符合指数衰减曲线y1=
,桶2中的水就是y2=a-
(k为常数),假设5分钟时,桶1和桶2中的水量相等.从注水开始时,经过m分钟时桶2中的水是桶1中水的3倍,则m=( )
| a |
| 2kt |
| a |
| 2kt |
| A、8 | B、10 | C、15 | D、20 |
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:由于5分钟后桶A和桶B中的水量相等,所以可求k=
,再利用,经过m分钟时桶2中的水是桶1中水的3倍,可求时间.
| 1 |
| 5 |
解答:
解:∵t=5时,y1=y2,∴由
=a-
,
得k=
.
∴y1=
∵经过m分钟时桶2中的水是桶1中水的3倍,
∴
=3(a-
),
∴m=10.
故选:B.
| a |
| 25k |
| a |
| 25k |
得k=
| 1 |
| 5 |
∴y1=
| a | ||
2
|
∵经过m分钟时桶2中的水是桶1中水的3倍,
∴
| a | ||
2
|
| a | ||
2
|
∴m=10.
故选:B.
点评:本题主要考查指数函数的实际应用,关键是根据题意,求出指数函数,进而解决问题.

练习册系列答案
相关题目
在研究某种线性相关问题时获得5组数据(x,y)(x为解释变量,y为预报变量),并根据这五组数据得到线性回归方程
=7x-2,如果已知前四组数据依次为(1,5)(3,20),(4,30),(5,25),第五组数据不慎丢失,但知道该组数据为(7,m),则m的值为( )
 |
| y |
| A、47 | B、48 | C、49 | D、50 |
双曲线x2-y2=1的离心率为( )
A、
| ||
| B、2 | ||
| C、4 | ||
| D、1 |
空间四边形ABCD中,M、N分别为对角线BD和AC的中点,AB=CD=2,MN=
,则AB与CD所成的角为( )
| 3 |
| A、30° | B、60° |
| C、90° | D、120° |
已知直线l:xsinθ-ycosθ+sinθ+λ=0,下列命题中真命题序号为( )
①直线l的斜率为tanθ;
②存在实数λ,使得对任意的θ,直线l恒过定点;
③对任意非零实数λ,都有对任意的θ,直线l与同一个定圆相切;
④若圆O:(x+1)2+y2=4上到直线l距离为1的点恰好3个,则λ=±1.
①直线l的斜率为tanθ;
②存在实数λ,使得对任意的θ,直线l恒过定点;
③对任意非零实数λ,都有对任意的θ,直线l与同一个定圆相切;
④若圆O:(x+1)2+y2=4上到直线l距离为1的点恰好3个,则λ=±1.
| A、①② | B、②③ |
| C、②③④ | D、①③④ |
抛物线y2=2px(p>0)的焦点为F,A为抛物线上一点,则以A为圆心,AF为半径的圆与抛物线的准线的位置关系为( )
| A、相交 | B、相切 |
| C、相离 | D、以上都有可能 |
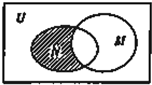 设全集U为实数集R,M={x|x>2},N={x|x<4},则图中阴影部分所表示的集合是( )
设全集U为实数集R,M={x|x>2},N={x|x<4},则图中阴影部分所表示的集合是( )| A、{x|x≤2} |
| B、{x|x≥4} |
| C、{x|x<2} |
| D、{x|2<x<4} |