题目内容
在△ABC中，a=
，b=
，A=
，则（ ）
| 5 |
| 15 |
| π |
| 6 |
A、c=2
| ||||
B、c=
| ||||
C、c=2
| ||||
| D、以上都不正确 |
考点：正弦定理
专题：解三角形
分析：利用余弦定理列出关系式，将a，b，cosA的值代入即可确定出c的值．
解答：
解：∵在△ABC中，a=
，b=
，A=
，
∴由余弦定理得：a2=b2+c2-2bccosA，即5=15+c2-3
c，
解得：c=2
或c=
，
故选：C．
| 5 |
| 15 |
| π |
| 6 |
∴由余弦定理得：a2=b2+c2-2bccosA，即5=15+c2-3
| 5 |
解得：c=2
| 5 |
| 5 |
故选：C．
点评：此题考查了余弦定理，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
双曲线x2-y2=1的离心率为（ ）
A、
| ||
| B、2 | ||
| C、4 | ||
| D、1 |
在△ABC中，内角A，B，C的对边分别为a，b，c，若a2-b2+c2+ac=0则角B的大小为（ ）
| A、120° | B、30° |
| C、60° | D、150° |
若θ=
（0≤k≤10，k∈Z），则sinθ+cosθ≥1的概率为（ ）
| kπ |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知数列{an}的通项an=n2（cos2
-sin2
），其前n项和为Sn，则S60=（ ）
| nπ |
| 3 |
| nπ |
| 3 |
| A、1840 | B、1880 |
| C、1960 | D、1980 |
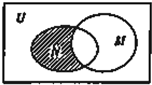设全集U为实数集R，M={x|x＞2}，N={x|x＜4}，则图中阴影部分所表示的集合是（ ）| A、{x|x≤2} |
| B、{x|x≥4} |
| C、{x|x＜2} |
| D、{x|2＜x＜4} |
在复平面内，复数2i（1+3i）对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
平面向量
与
的夹角为150°，
=（2，0），|
|=2，则|
+
|=（ ）
| a |
| b |
| a |
| b |
| a |
| 3 |
| b |
A、
| ||
| B、2 | ||
C、2
| ||
| D、4 |
等差数列{an}中，前n项和为Sn，若S16-S5=165则a9+a8+a16=（ ）
| A、90 | B、-80 | C、75 | D、45 |