题目内容
若P(2,-1)为圆
(θ为参数且0≤θ<2π)的弦的中点,则该弦所在的直线方程为( )
|
| A、x-y-3=0 |
| B、x+2y=5 |
| C、x+y-1=0 |
| D、2x-y-5=0 |
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:把参数方程化为直角坐标方程的方法,直线和圆相交的性质,求出所求直线的斜率,再用点斜式求出要求的直线的方程.
解答:
解:把圆
(θ为参数且0≤θ<2π)消去参数,化为直角坐标方程为 (x-1)2+y2=25,表示以C(1,0)为圆心、半径等于5的圆.
再根据所求直线和直线CP垂直,可得所求直线的斜率为-
=-
=1,可得所求直线的方程为y+1=1•(x-2),即 x-y-3=0,
故选:A.
|
再根据所求直线和直线CP垂直,可得所求直线的斜率为-
| 1 |
| KCP |
| 1 | ||
|
故选:A.
点评:本题主要考查把参数方程化为直角坐标方程的方法,直线和圆相交的性质,用点斜式求直线的方程,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
空间四边形ABCD中,M、N分别为对角线BD和AC的中点,AB=CD=2,MN=
,则AB与CD所成的角为( )
| 3 |
| A、30° | B、60° |
| C、90° | D、120° |
已知Sn和Tn分别是等差数列{an}和{bn}的前n项和,且
=
,则
=( )
| Sn |
| Tn |
| n |
| 2n+1 |
| a1+a2+a9+a12 |
| b4+b8 |
A、
| ||
B、
| ||
C、
| ||
D、
|
某人射击两次,第一次射中的概率为0.6,第二次射中的概率为0.7,则至少射中一次的概率为( )
| A、0.42 | B、0.46 |
| C、0.58 | D、0.88 |
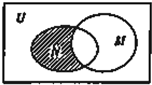 设全集U为实数集R,M={x|x>2},N={x|x<4},则图中阴影部分所表示的集合是( )
设全集U为实数集R,M={x|x>2},N={x|x<4},则图中阴影部分所表示的集合是( )| A、{x|x≤2} |
| B、{x|x≥4} |
| C、{x|x<2} |
| D、{x|2<x<4} |
椭圆C1:
+
=1和椭圆C2:
+
=1(0<k<9)有( )
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 9-k |
| y2 |
| 25-k |
| A、等长的长轴 |
| B、等长的焦距 |
| C、相等的离心率 |
| D、等长的短轴 |
已知数列{an}中,an-an-1=2(n≥2),且a1=1,则此数列的第10项是( )
| A、18 | B、19 | C、20 | D、21 |
 如图,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,且AE=EF=FB=5,DE=12,动点P从点A出发,沿折线AD-DC-CB以每秒1个单位长的速度运动到点B停止,设运动时间为t秒,y=S△EPF,则y与t的函数图象大致是( )
如图,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,且AE=EF=FB=5,DE=12,动点P从点A出发,沿折线AD-DC-CB以每秒1个单位长的速度运动到点B停止,设运动时间为t秒,y=S△EPF,则y与t的函数图象大致是( )


