题目内容
设曲线y=x3-3x2+1在点P（1，-1）处的切线与直线ax+y+1=0垂直，则实数a等于（ ）
| A、3 | ||
B、
| ||
| C、-3 | ||
D、-
|
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：求导函数，求得切线的斜率，利用曲线在点P（1，-1）处的切线与直线ax+y+1=0互相垂直，即可求得结论．
解答：
解：y=x3-3x2+1，可得y′=3x2-6x，
当x=1时，y′=3-6=-3，
∵曲线在点P（1，-1）处的切线与直线ax+y+1=0互相垂直，
∴-3•（-a）=-1
∴a=-
．
故选D．
当x=1时，y′=3-6=-3，
∵曲线在点P（1，-1）处的切线与直线ax+y+1=0互相垂直，
∴-3•（-a）=-1
∴a=-
| 1 |
| 3 |
故选D．
点评：本题考查导数的几何意义，考查两直线的位置关系，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
已知直线l：xsinθ-ycosθ+sinθ+λ=0，下列命题中真命题序号为（ ）
①直线l的斜率为tanθ；
②存在实数λ，使得对任意的θ，直线l恒过定点；
③对任意非零实数λ，都有对任意的θ，直线l与同一个定圆相切；
④若圆O：（x+1）2+y2=4上到直线l距离为1的点恰好3个，则λ=±1．
①直线l的斜率为tanθ；
②存在实数λ，使得对任意的θ，直线l恒过定点；
③对任意非零实数λ，都有对任意的θ，直线l与同一个定圆相切；
④若圆O：（x+1）2+y2=4上到直线l距离为1的点恰好3个，则λ=±1．
| A、①② | B、②③ |
| C、②③④ | D、①③④ |
若θ=
（0≤k≤10，k∈Z），则sinθ+cosθ≥1的概率为（ ）
| kπ |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
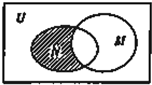设全集U为实数集R，M={x|x＞2}，N={x|x＜4}，则图中阴影部分所表示的集合是（ ）| A、{x|x≤2} |
| B、{x|x≥4} |
| C、{x|x＜2} |
| D、{x|2＜x＜4} |
在复平面内，复数2i（1+3i）对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知数列{an}中，an-an-1=2（n≥2），且a1=1，则此数列的第10项是（ ）
| A、18 | B、19 | C、20 | D、21 |
平面向量
与
的夹角为150°，
=（2，0），|
|=2，则|
+
|=（ ）
| a |
| b |
| a |
| b |
| a |
| 3 |
| b |
A、
| ||
| B、2 | ||
C、2
| ||
| D、4 |
已知A（1，1），B（3，5），则直线AB的垂直平分线为（ ）
| A、x-2y-8=0 |
| B、2x+y+8=0 |
| C、x+2y-8=0 |
| D、2x-y-8=0 |