题目内容
设某种动物的体重y(单位:千克)与身长x(单位:厘米)具有线性相关关系,根据一组样本数据建立的回归直线方程为
=0.85x-85.71,则下列结论中不正确的是( )
 |
| y |
| A、y与x具有正的线性相关关系 | ||||
B、回归直线必定经过样本中心点(
| ||||
| C、若某一种该种动物身长增加1厘米,则其体重必定为0.85千克 | ||||
| D、若某一只该种动物身长170厘米,则其体重必定为58.79千克 |
考点:线性回归方程
专题:概率与统计
分析:根据回归方程为
=0.85x-85.71,0.85>0,可知A,B,C均正确,对于D回归方程只能进行预测,但不可断定.
 |
| y |
解答:
解:对于A,0.85>0,所以y与x具有正的线性相关关系,故正确;
对于B,回归直线过样本点的中心(
,
),故正确;
对于C,∵回归方程为
=0.85x-85.71,∴该大学某女生身高增加1cm,则其体重约增加0.85kg,故正确;
对于D,x=170cm时,
=0.85x-85.71=0.85×170-85.71=58.79,但这是预测值,不可断定其体重为58.79kg,故不正确
故选:D.
对于B,回归直线过样本点的中心(
. |
| x |
. |
| y |
对于C,∵回归方程为
 |
| y |
对于D,x=170cm时,
 |
| y |
故选:D.
点评:本题考查线性回归方程,考查学生对线性回归方程的理解,属于中档题.

练习册系列答案
相关题目
在研究某种线性相关问题时获得5组数据(x,y)(x为解释变量,y为预报变量),并根据这五组数据得到线性回归方程
=7x-2,如果已知前四组数据依次为(1,5)(3,20),(4,30),(5,25),第五组数据不慎丢失,但知道该组数据为(7,m),则m的值为( )
 |
| y |
| A、47 | B、48 | C、49 | D、50 |
抛物线y2=2px(p>0)的焦点为F,A为抛物线上一点,则以A为圆心,AF为半径的圆与抛物线的准线的位置关系为( )
| A、相交 | B、相切 |
| C、相离 | D、以上都有可能 |
已知Sn和Tn分别是等差数列{an}和{bn}的前n项和,且
=
,则
=( )
| Sn |
| Tn |
| n |
| 2n+1 |
| a1+a2+a9+a12 |
| b4+b8 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若θ=
(0≤k≤10,k∈Z),则sinθ+cosθ≥1的概率为( )
| kπ |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
某人射击两次,第一次射中的概率为0.6,第二次射中的概率为0.7,则至少射中一次的概率为( )
| A、0.42 | B、0.46 |
| C、0.58 | D、0.88 |
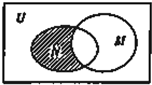 设全集U为实数集R,M={x|x>2},N={x|x<4},则图中阴影部分所表示的集合是( )
设全集U为实数集R,M={x|x>2},N={x|x<4},则图中阴影部分所表示的集合是( )| A、{x|x≤2} |
| B、{x|x≥4} |
| C、{x|x<2} |
| D、{x|2<x<4} |
已知数列{an}中,an-an-1=2(n≥2),且a1=1,则此数列的第10项是( )
| A、18 | B、19 | C、20 | D、21 |