题目内容
已知
=(cos(α+β),sin(α+β)),
=(cosβ,sinβ),且|
-
|=1,求
(1)cosα的值;
(2)在[0,π]内,求∠α的度数.
| a |
| b |
. |
| a |
| b |
(1)cosα的值;
(2)在[0,π]内,求∠α的度数.
考点:平面向量数量积的运算
专题:计算题,三角函数的求值,平面向量及应用
分析:(1)求出向量a,b的模和数量积,再由向量的平方即为模的平方,即可得到;
(2)由特殊角的三角函数值,即可得到角α.
(2)由特殊角的三角函数值,即可得到角α.
解答:
解:(1)由于
=(cos(α+β),sin(α+β)),
=(cosβ,sinβ),
且|
-
|=1,
则|
|=|
|=1,
•
=cos(α+β)cosβ+sin(α+β)sinβ=cos(α+β-β)=cosα,
则有|
-
|2=
2-2
•
+
2=1-2cosα+1=1,
则cosα=
;
(2)在[0,π]内,由于cosα=
,
则∠α=
.
| a |
| b |
且|
. |
| a |
| b |
则|
| a |
| b |
| a |
| b |
则有|
. |
| a |
| b |
| a |
| a |
| b |
| b |
则cosα=
| 1 |
| 2 |
(2)在[0,π]内,由于cosα=
| 1 |
| 2 |
则∠α=
| π |
| 3 |
点评:本题考查平面向量的数量积的坐标公式和性质,考查三角函数的两角差的余弦公式,考查运算能力,属于基础题.

练习册系列答案
相关题目
已知数列{an}的前n项和为Sn,已知a1=2,且nSn+1-(n+1)Sn=n(n+1)(n∈N+),则过A(n,an)和B(n+2,an+2)的直线的一个方向向量的坐标可以是( )
| A、(2,-4) | ||||
| B、(-1,-1) | ||||
C、(-
| ||||
D、(1,-
|
方程ln(x+1)-
=0,(x>0)的根存在的大致区间是( )
| 2 |
| x |
| A、(0,1) |
| B、(1,2) |
| C、(2,e) |
| D、(3,4) |
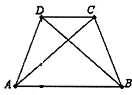 在等腰梯形ABCD中,AB∥CD,且AB>CD.设以A,B为焦点且过点D的双曲线的离心率为2,以C,D为焦点且过点A的椭圆的离心率e等于( )
在等腰梯形ABCD中,AB∥CD,且AB>CD.设以A,B为焦点且过点D的双曲线的离心率为2,以C,D为焦点且过点A的椭圆的离心率e等于( )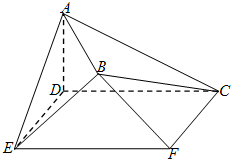 如图,在空间几何体AB-CDEF中,底面CDEF为矩形,DE=1,CD=2,AD⊥底面CDEF,AD=1,平面BEF⊥底面CDEF,且BE=BF=
如图,在空间几何体AB-CDEF中,底面CDEF为矩形,DE=1,CD=2,AD⊥底面CDEF,AD=1,平面BEF⊥底面CDEF,且BE=BF=