题目内容
已知：f（x）-cos（
π+2x）+cos（
π-2x）+2
sin（
+2x）（x∈R，n∈Z），
（1）求函数f（x）的值域和最小正周期；
（2）写出f（x）的单调递增区间．
| 6n+1 |
| 3 |
| 6n-1 |
| 3 |
| 3 |
| π |
| 3 |
（1）求函数f（x）的值域和最小正周期；
（2）写出f（x）的单调递增区间．
考点：两角和与差的正弦函数,三角函数的周期性及其求法,正弦函数的单调性
专题：三角函数的图像与性质
分析：（1）先利用正弦的两角和公式对函数解析式进行化简整理，进而根据三角函数的性质和周期公式求得函数的值域及最小正周期．
（2）根据余弦函数的性质求得函数的单调增区间．
（2）根据余弦函数的性质求得函数的单调增区间．
解答：
解：f（x）=cos（2nπ+
+2x）+cos（2nπ-
-2x）+2
sin（
+2x）=2cos(
+2x)+2
sin(
+2x)=4cos2x，
（1）函数f（x）的值域为[-4，4]，
函数f（x）的最小正周期 T=
=π，
（2）∵2kπ-π≤2x≤2kπ，（k∈Z），
∴kπ-
≤x≤kπ，
∴f（x）的单调递增区间为[kπ-
，kπ]（k∈Z）．
| π |
| 3 |
| π |
| 3 |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 3 |
| π |
| 3 |
（1）函数f（x）的值域为[-4，4]，
函数f（x）的最小正周期 T=
| 2π |
| ω |
（2）∵2kπ-π≤2x≤2kπ，（k∈Z），
∴kπ-
| π |
| 2 |
∴f（x）的单调递增区间为[kπ-
| π |
| 2 |
点评：本题主要考查了三角函数恒等变换的应用，三角函数图象和性质．考查了学生对三角函数图象的理解和基本公式的记忆．
练习册系列答案
相关题目
下列函数中增加得最快的是（ ）
| A、y=2x |
| B、y=3x |
| C、y=4x |
| D、y=ex |
已知F1，F2分别为双曲线
-
=1（a＞0，b＞0）的左、右焦点，O为原点，A为右顶点，P为双曲线左支上的任意一点，若
存在最小值为12a，则双曲线离心率e的取值范围是 （ ）
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1|-|OA| |
| A、[5，+∞） |
| B、（2，5] |
| C、（1，5] |
| D、（1，2） |
在△ABC中，角A=30°，B=60°，则b：c=（ ）
| A、1：2 | ||
| B、2：3 | ||
C、1：
| ||
D、
|
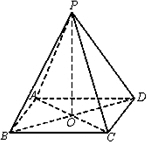如图，在四棱锥P-ABCD中，底面ABCD是矩形，四条侧棱长均相等且BD交AC于点O．